题目内容
已知中心在坐标原点,焦点在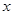 轴上的椭圆过点
轴上的椭圆过点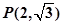 ,且它的离心率
,且它的离心率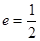 .
.

(1)求椭圆的标准方程;
(2)与圆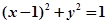 相切的直线
相切的直线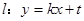 交椭圆于
交椭圆于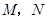 两点,若椭圆上一点
两点,若椭圆上一点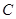 满足
满足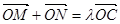 ,求实数
,求实数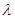 的取值范围.
的取值范围.
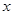 轴上的椭圆过点
轴上的椭圆过点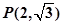 ,且它的离心率
,且它的离心率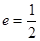 .
.
(1)求椭圆的标准方程;
(2)与圆
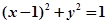 相切的直线
相切的直线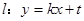 交椭圆于
交椭圆于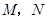 两点,若椭圆上一点
两点,若椭圆上一点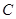 满足
满足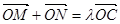 ,求实数
,求实数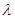 的取值范围.
的取值范围.(1)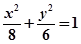 ;(2)
;(2)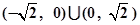 .
.
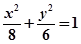 ;(2)
;(2)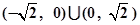 .
.试题分析:(1)设椭圆的标准方程为
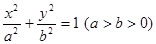 ,由已知得
,由已知得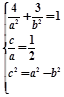 ,解出即可求得a,b;
,解出即可求得a,b;(2)由直线l:y=kx+t与圆(x+1)2+y2=1相切,可得k,t的关系式①,把y=kx+t代入
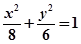 消掉y得x的二次方程,设M(x1,y1),N(x2,y2),由
消掉y得x的二次方程,设M(x1,y1),N(x2,y2),由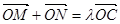 得λ
得λ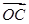 =(x1+x2,y1+y2),代入韦达定理可求得C点坐标,把点C代入椭圆方程可用k,t表示出λ,再由①式消掉k得关于t的函数,由t2范围可求得λ2的范围,进而求得λ的范围;.
=(x1+x2,y1+y2),代入韦达定理可求得C点坐标,把点C代入椭圆方程可用k,t表示出λ,再由①式消掉k得关于t的函数,由t2范围可求得λ2的范围,进而求得λ的范围;.试题解析:(1)设椭圆的标准方程为
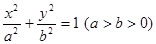
由已知得:
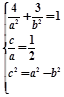 解得
解得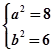 ,所以椭圆的标准方程为:
,所以椭圆的标准方程为: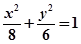
(2)因为直线
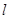 :
: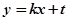 与圆
与圆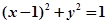 相切所以,
相切所以,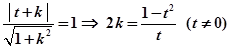
把
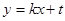 代入
代入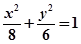 并整理得:
并整理得: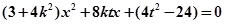 ┈7分
┈7分设
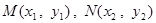 ,则有
,则有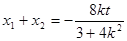
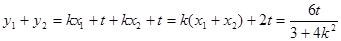
因为,
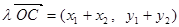 ,所以,
,所以,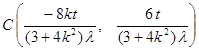
又因为点
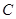 在椭圆上,所以,
在椭圆上,所以,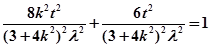
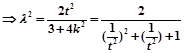 因为
因为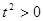 所以
所以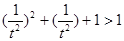
所以
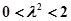 ,所以
,所以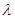 的取值范围为
的取值范围为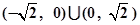

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
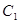 以双曲线
以双曲线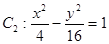 的实轴为短轴、虚轴为长轴,且与抛物线
的实轴为短轴、虚轴为长轴,且与抛物线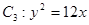 交于
交于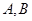 两点.
两点.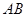 的长;
的长;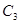 图像的公共区域内,是否存在一点
图像的公共区域内,是否存在一点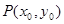 ,使得
,使得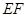 与
与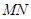 相互垂直平分于点
相互垂直平分于点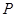 ?若存在,求点
?若存在,求点



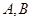 分别为椭圆
分别为椭圆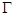 :
: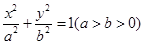 的左右顶点,
的左右顶点,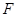 为右焦点,
为右焦点,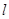 为
为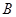 处的切线,
处的切线,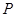 为
为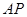 交
交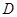 ,
,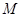 为
为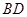 中点,有如下结论:①
中点,有如下结论:①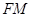 平分
平分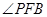 ;②
;②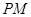 与椭圆
与椭圆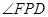 ;④使得
;④使得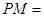
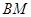 的点
的点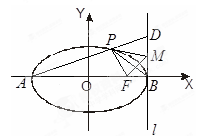
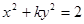 表示焦点在
表示焦点在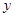 轴上的椭圆,那么实数
轴上的椭圆,那么实数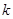 的取值范围是( )
的取值范围是( )



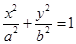
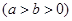 的焦点垂直于
的焦点垂直于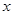 轴的弦长为
轴的弦长为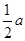 ,则双曲线
,则双曲线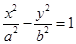 的离心率
的离心率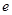 的值是( )
的值是( )


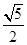
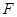 为椭圆
为椭圆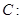
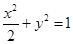 的左焦点,点
的左焦点,点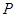 为椭圆
为椭圆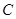 上任意一点,点
上任意一点,点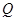 的坐标为
的坐标为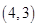 ,则
,则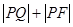 取最大值时,点
取最大值时,点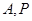 是椭圆
是椭圆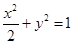 上两点,点
上两点,点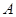 关于
关于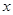 轴的对称点为
轴的对称点为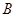 (异于点
(异于点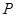 ),若直线
),若直线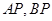 分别交
分别交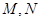 ,则
,则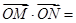 ( )
( )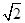
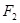 作垂直于实轴的弦
作垂直于实轴的弦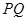 ,
,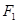 是另一焦点,若∠
是另一焦点,若∠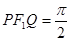 ,则椭圆的离心率
,则椭圆的离心率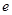 等于( )
等于( )


