题目内容
设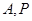 是椭圆
是椭圆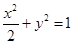 上两点,点
上两点,点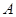 关于
关于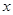 轴的对称点为
轴的对称点为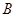 (异于点
(异于点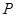 ),若直线
),若直线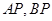 分别交
分别交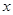 轴于点
轴于点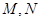 ,则
,则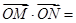 ( )
( )
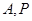 是椭圆
是椭圆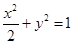 上两点,点
上两点,点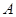 关于
关于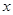 轴的对称点为
轴的对称点为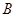 (异于点
(异于点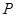 ),若直线
),若直线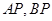 分别交
分别交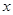 轴于点
轴于点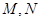 ,则
,则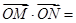 ( )
( )| A.0 | B.1 | C.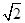 | D.2 |
D
试题分析:(特例法)不妨设
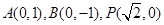 ,则
,则 ,
,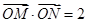 .选D.
.选D.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
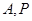 是椭圆
是椭圆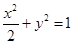 上两点,点
上两点,点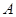 关于
关于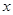 轴的对称点为
轴的对称点为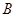 (异于点
(异于点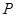 ),若直线
),若直线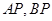 分别交
分别交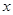 轴于点
轴于点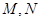 ,则
,则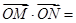 ( )
( )| A.0 | B.1 | C.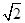 | D.2 |
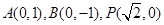 ,则
,则 ,
,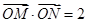 .选D.
.选D.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案