题目内容
(本小题满分14分)
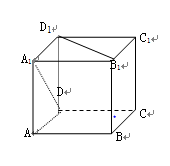
如图,正方体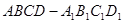 的棱长为
的棱长为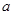 ,
,
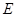 为
为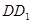 的中点(1)求证:
的中点(1)求证: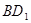 //平面
//平面 ;(2)求点
;(2)求点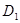 到平面
到平面 的距离
的距离 
如图,正方体
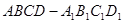 的棱长为
的棱长为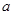 ,
,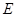 为
为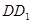 的中点(1)求证:
的中点(1)求证: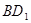 //平面
//平面 ;(2)求点
;(2)求点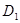 到平面
到平面 的距离
的距离 
解法一:(1)证明:连接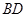 交
交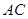 于
于 ,连
,连 . -------------------------------------2分
. -------------------------------------2分
因为 为正方形
为正方形 对角线的交点,
对角线的交点,

所以 为
为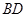 、
、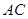 的中点. ------------------------------------------------------3分
的中点. ------------------------------------------------------3分
在D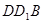 中,
中,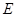 、
、 分别为
分别为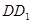 、
、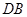 的中点,
的中点,
所以 //
//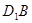 . ----------------------------5分
. ----------------------------5分
又
 平面
平面 ,
,
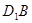
 平面
平面 ,
,
所以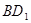 //平面
//平面 . --------------------------7分
. --------------------------7分
(2)解:设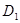 到平面
到平面 的距离为
的距离为 .
.
在 中,
中,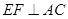 ,且
,且 ,
,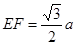 ,
,
所以 , ----------------------------------------------------9分
, ----------------------------------------------------9分
于是 . ----------------------------------------------------10分
. ----------------------------------------------------10分
因为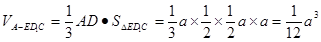 . --------------------------12分
. --------------------------12分
又 ,即
,即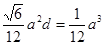 , --------------------------------------------13分
, --------------------------------------------13分
解得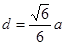 ,
,
故点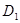 到平面
到平面 的距离为
的距离为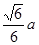 . ----------------------------------------------------14分
. ----------------------------------------------------14分
解法二:(1)如图所示建立空间直角坐标系,则
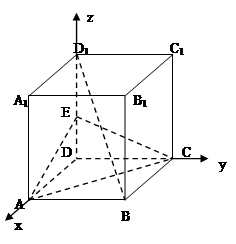
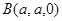 ,
, ,
,  ,
,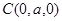 ,
, ,
,
故 ,
, ,
, ----------------------------2分
----------------------------2分
设平面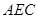 的法向量
的法向量 ,则
,则
 - --------------------------- ---------------------------3分
- --------------------------- ---------------------------3分
即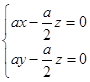 ,令
,令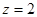 ,则
,则
∴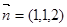 -----------------------------4分
-----------------------------4分
∵ ,∴
,∴ , ------------------------6分
, ------------------------6分
又∵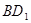
 平面
平面 ,所以
,所以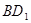 //平面
//平面 . ----------------------------7分
. ----------------------------7分
(2)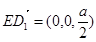 , ---------------------------------------------------------------9分
, ---------------------------------------------------------------9分
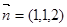 是平面
是平面 的一个法向量.
的一个法向量.
∴点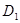 到平面
到平面 的距离
的距离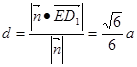 .--------------------------------------14分
.--------------------------------------14分
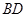 交
交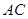 于
于 ,连
,连 . -------------------------------------2分
. -------------------------------------2分因为
 为正方形
为正方形 对角线的交点,
对角线的交点,
所以
 为
为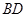 、
、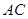 的中点. ------------------------------------------------------3分
的中点. ------------------------------------------------------3分在D
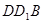 中,
中,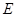 、
、 分别为
分别为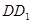 、
、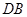 的中点,
的中点,所以
 //
//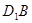 . ----------------------------5分
. ----------------------------5分又

 平面
平面 ,
,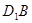
 平面
平面 ,
,所以
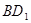 //平面
//平面 . --------------------------7分
. --------------------------7分(2)解:设
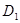 到平面
到平面 的距离为
的距离为 .
.在
 中,
中,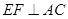 ,且
,且 ,
,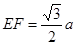 ,
,所以
 , ----------------------------------------------------9分
, ----------------------------------------------------9分于是
 . ----------------------------------------------------10分
. ----------------------------------------------------10分因为
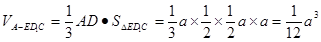 . --------------------------12分
. --------------------------12分又
 ,即
,即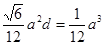 , --------------------------------------------13分
, --------------------------------------------13分解得
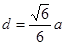 ,
, 故点
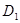 到平面
到平面 的距离为
的距离为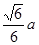 . ----------------------------------------------------14分
. ----------------------------------------------------14分解法二:(1)如图所示建立空间直角坐标系,则
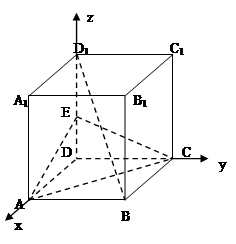
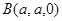 ,
, ,
,  ,
,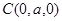 ,
, ,
,故
 ,
, ,
, ----------------------------2分
----------------------------2分设平面
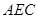 的法向量
的法向量 ,则
,则 - --------------------------- ---------------------------3分
- --------------------------- ---------------------------3分即
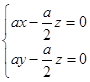 ,令
,令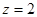 ,则
,则
∴
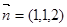 -----------------------------4分
-----------------------------4分∵
 ,∴
,∴ , ------------------------6分
, ------------------------6分又∵
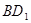
 平面
平面 ,所以
,所以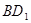 //平面
//平面 . ----------------------------7分
. ----------------------------7分(2)
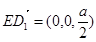 , ---------------------------------------------------------------9分
, ---------------------------------------------------------------9分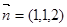 是平面
是平面 的一个法向量.
的一个法向量.∴点
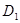 到平面
到平面 的距离
的距离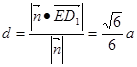 .--------------------------------------14分
.--------------------------------------14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


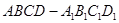 中,
中,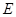 为线段
为线段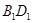 上的一个动点,则下列结论中错误的是( )
上的一个动点,则下列结论中错误的是( )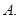 、
、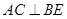
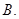 、
、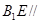 平面
平面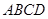
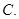 、三棱锥
、三棱锥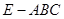 的体积为定值
的体积为定值 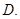 、直线
、直线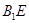
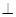 直线
直线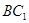
 的棱长为1,E为棱
的棱长为1,E为棱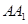 的中点,一直线过
的中点,一直线过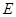 点与异面直线
点与异面直线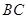 ,
,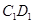 分别相交与
分别相交与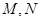 两点,则线段
两点,则线段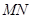 的长等于 ( )
的长等于 ( )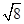
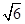
 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, 分别是
分别是 的中点,DE⊥面CBB1.
的中点,DE⊥面CBB1.  与圆柱
与圆柱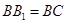 ,求
,求 与面
与面 所成角的正弦值.
所成角的正弦值.
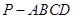 中
中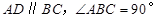 ,
,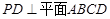 ,
,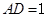 ,
,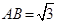 ,
,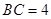 .
.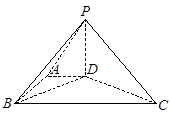
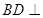
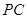 ;
;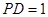 时,求此四棱锥的表面积.
时,求此四棱锥的表面积.
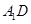 与直线
与直线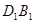 所成的角为_________;
所成的角为_________;