题目内容
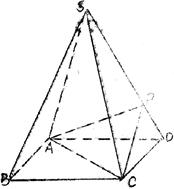
(本小题满分14分)如图, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, 分别是
分别是 的中点,DE⊥面CBB1.
的中点,DE⊥面CBB1.
(Ⅰ)证明:DE //面ABC;
(Ⅱ)求四棱锥 与圆柱
与圆柱 的体积比;
的体积比;
(Ⅲ)若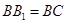 ,求
,求 与面
与面 所成角的正弦值.
所成角的正弦值.

 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, 分别是
分别是 的中点,DE⊥面CBB1.
的中点,DE⊥面CBB1. (Ⅰ)证明:DE //面ABC;
(Ⅱ)求四棱锥
 与圆柱
与圆柱 的体积比;
的体积比;(Ⅲ)若
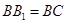 ,求
,求 与面
与面 所成角的正弦值.
所成角的正弦值.
解:
 证明:连结
证明:连结 .
. 分别为
分别为 的中点,∴
的中点,∴ .…2分
.…2分又
 ,且
,且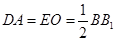 .
.∴四边形
 是平行四边形,
是平行四边形,即
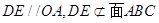 .………………3分
.………………3分∴
 .………………4分
.………………4分
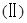 ∵
∵ ,且由
,且由 知
知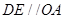 .
.∴
 ,∴
,∴ ,∴
,∴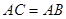 .………………6分
.………………6分因
 是底面圆
是底面圆 的直径,得
的直径,得 ,且
,且 ,
,∴
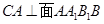 即
即 为四棱锥的高. ………………………………7分
为四棱锥的高. ………………………………7分设圆柱高为
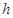 ,底半径为
,底半径为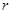 ,则
,则 ,
,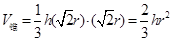 ,
,∴
 .………………………………9分
.………………………………9分 解一:由
解一:由 可知,可分别以
可知,可分别以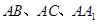 为
为坐标轴建立空间直角标系,如图设
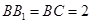 ,
,则
 ,
,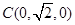 ,
,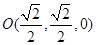 ,
,从而
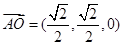 ,
, ,由题设知
,由题设知 是面
是面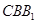 的法向量,
的法向量,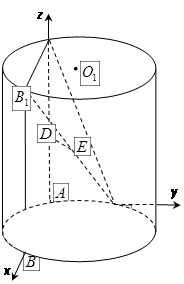
设所求的角为
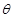 .…………………………………12分则
.…………………………………12分则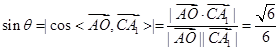 .………………………………14分
.………………………………14分
解二:作过
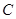 的母线
的母线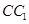 ,连结
,连结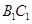 ,则
,则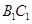 是上底
是上底面圆
 的直径,连结
的直径,连结 ,得
,得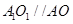 ,
,又
 ,∴
,∴ ,连结
,连结 ,
,则
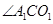 为
为 与面
与面 所成的角,
所成的角,设
 ,则
,则 ,
,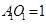 .(12分),
.(12分),在
 中,
中, .(14分)
.(14分)略

练习册系列答案
相关题目
 中,
中,  ,
, 平面
平面 ,点
,点 是
是 的中点.
的中点. ;
; 平面
平面 ;
;
 是空间三条直线,则下列命题正确的是………………………( )
是空间三条直线,则下列命题正确的是………………………( ) ,
, ,则
,则 ;
; ,
, ,则
,则 上,且到
上,且到 ;
;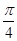 .
.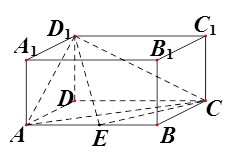
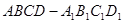 的棱长为
的棱长为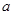 ,
,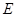 为
为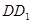 的中点(1)求证:
的中点(1)求证: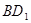 //平面
//平面 ;(2)求点
;(2)求点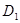 到平面
到平面
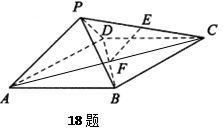
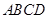 沿对角线
沿对角线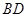 折成直二面角后,有下列四个结论:
折成直二面角后,有下列四个结论: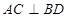 (2)
(2)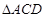 是等边三角形
是等边三角形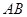 与平面
与平面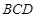 的夹角成60° (4)
的夹角成60° (4) 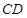 所成的角为60°
所成的角为60° a、
a、 a,其余四根均为a,用它们搭成三棱锥,则其中两条较长的棱所在的直线的夹角的余弦值为
a,其余四根均为a,用它们搭成三棱锥,则其中两条较长的棱所在的直线的夹角的余弦值为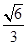
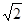 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。 D的大小
D的大小