题目内容
(12分)如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,
求证:平面A B1D1∥平面EFG;
(2) 求证:平面AA1C⊥面EFG.

求证:平面A B1D1∥平面EFG;
(2) 求证:平面AA1C⊥面EFG.

见解析。
(1)∵E,F,G分别是CB,CD,CC1的中点
∴FG∥C1D,EG∥BC1,EF∥BD
∴平面EFG∥平面BC1D
又∵BD∥B1D1,C1D∥AB1,BC1∥AD1
∴平面BC1D∥AB1D1
∴平面AB1D1∥平面EFG
(2)∵EF∥BD ,ABCD为正方形
∴BD⊥AC, 即EF⊥AC
又∵正方体中AA1⊥面ABCD,EF属于面ABCD
∴AA1⊥EF
∵AA1,AC属于面AA1C
∴EF⊥平面AA1C
又∵EF属于面EFG
∴平面AA1C⊥平面EFG。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
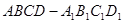 的棱长为
的棱长为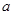 ,
,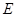 为
为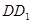 的中点(1)求证:
的中点(1)求证: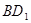 //平面
//平面 ;(2)求点
;(2)求点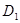 到平面
到平面
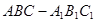 中,
中,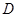 是
是 的中点,
的中点,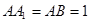
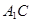 ∥平面
∥平面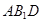 ;
;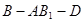 的大小.
的大小.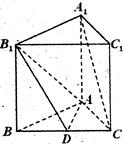
 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。 D的大小
D的大小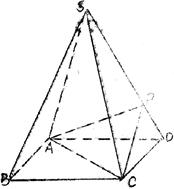
 中,
中,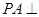 底面
底面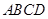 ,
,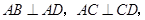
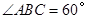 ,
,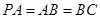 ,
,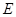 是
是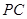 的中点.
的中点.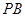 和平面
和平面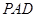 所成的角的大小;
所成的角的大小;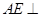 平面
平面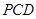 ;
;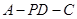 的正弦值.
的正弦值.
 , 线段
, 线段 中点的为
中点的为 ,且
,且 ,则异面线段
,则异面线段 B
B C.
C.  D.
D.

 若CM=BN=a(0<a<
若CM=BN=a(0<a<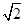 ).
).
 ⊥平面
⊥平面 ,
, ⊥平面
⊥平面