题目内容
(本题满分10分)
如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥底面ABCD,M为SA的中点,N为CD的中点.⑴证明:平面SBD⊥平面SAC;⑵证明:直线MN//平面SBC.

如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥底面ABCD,M为SA的中点,N为CD的中点.⑴证明:平面SBD⊥平面SAC;⑵证明:直线MN//平面SBC.

证明:⑴因为ABCD是菱形,所以BD⊥AC.----1分
因SA⊥底面ABCD,所以BD⊥SA.----------3分
因SA与AC交于点A,所以BD⊥面SAC.----4分
因BD 面SBD,所以面SBD⊥面SAC;------5分
面SBD,所以面SBD⊥面SAC;------5分
⑵取SB的中上E,连结ME、CE,
因M为SA中点,所以ME//AB且ME=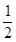 AB.
AB.
又ABCD是菱形,N为CD中点,
所以CN//AB且CN=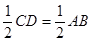 ,---------8分
,---------8分
所以CN//EM且CN=EM,
所以四边形CNME是平行四边形,所以MN//CE,
又MN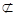 面SBC,CE
面SBC,CE 面SBC,所以MN//面SBC.------------------10分
面SBC,所以MN//面SBC.------------------10分
因SA⊥底面ABCD,所以BD⊥SA.----------3分
因SA与AC交于点A,所以BD⊥面SAC.----4分
因BD
 面SBD,所以面SBD⊥面SAC;------5分
面SBD,所以面SBD⊥面SAC;------5分⑵取SB的中上E,连结ME、CE,
因M为SA中点,所以ME//AB且ME=
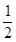 AB.
AB.又ABCD是菱形,N为CD中点,
所以CN//AB且CN=
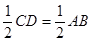 ,---------8分
,---------8分所以CN//EM且CN=EM,
所以四边形CNME是平行四边形,所以MN//CE,
又MN
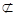 面SBC,CE
面SBC,CE 面SBC,所以MN//面SBC.------------------10分
面SBC,所以MN//面SBC.------------------10分略

练习册系列答案
相关题目

 中,
中,  ,
, 平面
平面 ,点
,点 是
是 的中点.
的中点. ;
; 平面
平面 ;
;


 为任何正数,均有
为任何正数,均有 ;
; .
. 
 是边长为
是边长为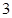 的正方形,
的正方形,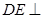 平面
平面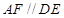 ,
,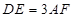 ,
,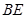 与平面
与平面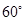 .
.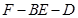 的余弦值;
的余弦值;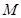 是线段
是线段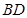 上的一个动点,问当
上的一个动点,问当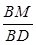 的值为多少时,可使得
的值为多少时,可使得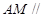 平面
平面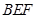 ,并证明你的结论.
,并证明你的结论.
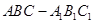 中,若
中,若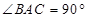 ,
,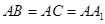 ,则异面直线
,则异面直线 与
与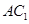 所成的角等于( )
所成的角等于( )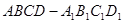 的棱长为
的棱长为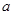 ,
,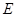 为
为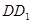 的中点(1)求证:
的中点(1)求证: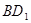 //平面
//平面 ;(2)求点
;(2)求点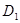 到平面
到平面





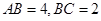 的矩形
的矩形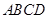 ,沿对角线
,沿对角线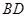 将
将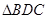 折起,使得面
折起,使得面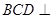 面
面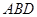 ,则异面直线
,则异面直线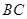 与
与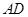 所成角的余弦值为
所成角的余弦值为