题目内容
3.设曲线y=$\frac{1}{x}$在点(1,1)处的切线与直线ax+y+1=0垂直,则a=( )| A. | 1 | B. | -1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
分析 由y=$\frac{1}{x}$,知y′|x=1=-1,由曲线y=$\frac{1}{x}$在点(1,1)处的切线与直线ax+y+1=0垂直,知-a=1,由此能求出a.
解答 解:∵y=$\frac{1}{x}$,
∴y′=-$\frac{1}{{x}^{2}}$,
∴y′|x=1=-1,
∵曲线y=$\frac{1}{x}$在点(1,1)处的切线与直线ax+y+1=0垂直,
∴-a=1,即a=-1.
故选:B.
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及导数的几何意义:在切点处的导数值即为切线的斜率,两直线垂直则斜率乘积为-1,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
11.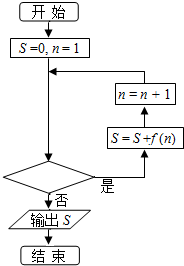 已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
 已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )| A. | n≤100? | B. | n≤99? | C. | n>100? | D. | n>99? |
15.对于非空集合A,B,定义运算:A⊕B={x|x∈A∪B,且x∉A∩B},已知M={x|a<x<b},N={x|c<x<d},其中a、b、c、d满足条件a+b=c+d,ab<cd<0,则M⊕N=( )
| A. | (a,d)∪(b,c) | B. | (c,a]∪[b,d) | C. | (a,c]∪[d,b) | D. | (c,a)∪(d,b) |
13.定义在(0,+∞)上的函数f(x)满足:?x∈(0,+∞),2f(x)<xf′(x)<3f(x)恒成立,其中f′(x)为f(x)的导函数,则( )
| A. | $\frac{1}{16}$<$\frac{f(1)}{f(2)}$<$\frac{1}{8}$ | B. | $\frac{1}{8}$<$\frac{f(1)}{f(2)}$<$\frac{1}{4}$ | C. | $\frac{1}{4}$<$\frac{f(1)}{f(2)}$<$\frac{1}{3}$ | D. | $\frac{1}{3}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ |
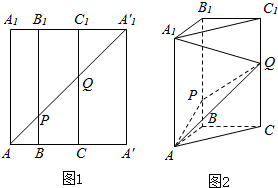 如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1′分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1中
如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1′分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1中