题目内容
13.定义在(0,+∞)上的函数f(x)满足:?x∈(0,+∞),2f(x)<xf′(x)<3f(x)恒成立,其中f′(x)为f(x)的导函数,则( )| A. | $\frac{1}{16}$<$\frac{f(1)}{f(2)}$<$\frac{1}{8}$ | B. | $\frac{1}{8}$<$\frac{f(1)}{f(2)}$<$\frac{1}{4}$ | C. | $\frac{1}{4}$<$\frac{f(1)}{f(2)}$<$\frac{1}{3}$ | D. | $\frac{1}{3}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ |
分析 分别构造函数g(x)=$\frac{f(x)}{{x}^{2}}$,x∈(0,+∞),h(x)=$\frac{f(x)}{{x}^{3}}$,x∈(0,+∞),利用导数研究其单调性即可得出.
解答 解:令g(x)=$\frac{f(x)}{{x}^{2}}$,x∈(0,+∞),
g′(x)=$\frac{x{f}^{′}(x)-2f(x)}{{x}^{3}}$,
∵?x∈(0,+∞),2f(x)<xf′(x)<3f(x)恒成立,
∴f(x)>0,
0<$\frac{x{f}^{′}(x)-2f(x)}{{x}^{3}}$,
∴g′(x)>0,
∴函数g(x)在x∈(0,+∞)上单调递增,
∴$\frac{f(1)}{1}$<$\frac{f(2)}{4}$,
∴$\frac{f(1)}{f(2)}$$<\frac{1}{4}$.
令h(x)=$\frac{f(x)}{{x}^{3}}$,x∈(0,+∞),
h′(x)=$\frac{x{f}^{′}(x)-3f(x)}{{x}^{4}}$,
∵?x∈(0,+∞),2f(x)<xf′(x)<3f(x)恒成立,
∴h′(x)=$\frac{x{f}^{′}(x)-3f(x)}{{x}^{4}}$<0,
∴函数h(x)在x∈(0,+∞)上单调递减,
∴$\frac{f(1)}{1}$>$\frac{f(2)}{8}$,
∴$\frac{1}{8}$<$\frac{f(1)}{f(2)}$.
综上可得:$\frac{1}{8}$<$\frac{f(1)}{f(2)}$$<\frac{1}{4}$.
故选:B.
点评 本题考查了利用导数研究其单调性极值与最值、构造函数法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设曲线y=$\frac{1}{x}$在点(1,1)处的切线与直线ax+y+1=0垂直,则a=( )
| A. | 1 | B. | -1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
2.sin70°cos10°+cos110°sin10°=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
3.已知集合A={x|ax2-3x+2=0,a∈R},若集合A中至多有一个元素,则实数a的值是( )
| A. | a=0 | B. | a≥$\frac{9}{8}$ | C. | a=0或a≥$\frac{9}{8}$ | D. | 不确定 |
 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$. 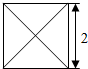 已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.
已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.