题目内容
8.已知圆C过点(0,2)且与直线x+$\sqrt{3}$y-4=0切于点$(1,\sqrt{3})$.(1)求圆C的方程;
(2)若P,Q为圆C与y轴的交点(P在Q上),过点T(0,4)的直线l交圆C于M,N两点,若M,N都不与P,Q重合时,是否存在定直线m,使得直线PN与QM的交点G恒在直线m上.若存在,求出直线m的方程;若不存在,说明理由.
分析 (1)根据圆的性质,结合条件建立方程关系即可求圆C的方程;
(2)联立直线和圆的方程,利用消参法进行转化即可.
解答 解:(1)设圆心C(a,b),
由题有$\left\{{\begin{array}{l}{\frac{{b-\sqrt{3}}}{a-1}=\sqrt{3}}\\{\sqrt{{{(a-1)}^2}+{{(b-\sqrt{3})}^2}}=\sqrt{{{(a-0)}^2}+{{(b-2)}^2}}}\end{array}}\right.$,得a=b=0,
所以,圆心为(0,0),半径为2,
故圆的方程为x2+y2=4
(2)根据圆的对称性,点G落在与y轴垂直的直线上
令N(-2,0),则直线$TN:\frac{x}{-2}+\frac{y}{4}=1?y=2x+4$与圆C:x2+y2=4联立得:5x2+16x+12=0,
∴${x_M}=-\frac{6}{5}$,∴$M(-\frac{6}{5},\frac{8}{5})$,QM:y=-3x-2
所以直线PN:x-y+2=0与QM的交点G(-1,1),
猜想点G落在定直线y=1上.
下证:$\left\{\begin{array}{l}y=kx+4\\{x^2}+{y^2}=4\end{array}\right.$得:(1+k2)x2+8kx+12=0$\left\{\begin{array}{l}△={(8k)^2}-48(1+{k^2})>0\\{x_1}+{x_2}=\frac{-8k}{{1+{k^2}}}\\{x_1}{x_2}=\frac{12}{{1+{k^2}}}\end{array}\right.$
直线PN:$\frac{y-2}{x}=\frac{{{y_1}-2}}{x_1}$,直线QM:$\frac{y+2}{x}=\frac{{{y_2}+2}}{x_2}$
消去x得:$\frac{y-2}{y+2}=\frac{{({y_1}-2){x_2}}}{{({y_2}+2){x_1}}}$
要证:G落在定直线y=1上,只需证:$\frac{1-2}{1+2}=\frac{{({y_1}-2){x_2}}}{{({y_2}+2){x_1}}}$
即证:$\frac{-1}{3}=\frac{{(k{x_1}+2){x_2}}}{{(k{x_2}+6){x_1}}}$
即证:-kx1x2-6x1=3kx1x2+6x2
即证:4kx1x2+6(x1+x2)=0
即证:$4k\frac{12}{{1+{k^2}}}-6\frac{8k}{{1+{k^2}}}=0$
显然成立.
所以直线PN与QM的交点在一条定直线上.
点评 本题主要考查直线和圆的位置关系的应用,根据条件求出圆的标准方程,以及利用直线和圆进行联立是解决本题的关键.综合性较强,有一定的难度.

| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰直角三角形 |
| A. | 1 | B. | -1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
| A. | f(2016)<0 | B. | f(2016)<e${\;}^{-201{6}^{2}}$ | ||
| C. | f(2)<0 | D. | f(2)>e-4032 |
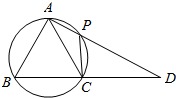 如图所示,在四边形ABCP中,线段AP与BC的延长线交于点D,已知AB=AC且A,B,C,P四点共圆.
如图所示,在四边形ABCP中,线段AP与BC的延长线交于点D,已知AB=AC且A,B,C,P四点共圆.