题目内容
12.对定义域分别为D1,D2的函数y=f(x),y=g(x),规定:函数h(x)=$\left\{\begin{array}{l}{f(x)•g(x),x∈{D}_{1}且x∈{D}_{2}}\\{f(x),x∈{D}_{1}且x∉{D}_{2}}\\{g(x),x∉{D}_{1}且x∈{D}_{2}}\end{array}\right.$.若f(x)=x-2(x≥1),g(x)=-2x+3(x≤2),则h(x)的解析式h(x)=$\left\{\begin{array}{l}{(x-2)(-2x+3),1≤x≤2}\\{x-2,x>2}\\{-2x+3,x<1}\end{array}\right.$.分析 由题中所给的新定义函数,根据其规则结合f(x)=x-2(x≥1),g(x)=-2x+3(x≤2),直接写出h(x)的解析式即可得到答案.
解答 解:由题意,函数h(x)=$\left\{\begin{array}{l}{f(x)•g(x),x∈{D}_{1}且x∈{D}_{2}}\\{f(x),x∈{D}_{1}且x∉{D}_{2}}\\{g(x),x∉{D}_{1}且x∈{D}_{2}}\end{array}\right.$,
∵f(x)=x-2(x≥1),g(x)=-2x+3(x≤2),
∴h(x)的解析式h(x)=$\left\{\begin{array}{l}{(x-2)(-2x+3),1≤x≤2}\\{x-2,x>2}\\{-2x+3,x<1}\end{array}\right.$,
故答案为:)=$\left\{\begin{array}{l}{(x-2)(-2x+3),1≤x≤2}\\{x-2,x>2}\\{-2x+3,x<1}\end{array}\right.$.
点评 本题是一个新定义的题,此类题解答的关键是理解新定义,根据新定义的规则进行变形可计算得到答案.

练习册系列答案
相关题目
2.下列变量间的关系属于线性关系的是( )
| A. | 球的体积与表面积之间的关系 | |
| B. | 正方形面积和它的边长之间的关系 | |
| C. | 家庭收入愈多,其消费支出也有增长的趋势 | |
| D. | 价格不变的条件下,商品销售额与销量量之间的关系 |
3.设曲线y=$\frac{1}{x}$在点(1,1)处的切线与直线ax+y+1=0垂直,则a=( )
| A. | 1 | B. | -1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
20.已知定义在R上的奇函数f(x),满足2016f(-x)<f′(x)恒成立,且f(1)=e-2016,则下列结论正确的是( )
| A. | f(2016)<0 | B. | f(2016)<e${\;}^{-201{6}^{2}}$ | ||
| C. | f(2)<0 | D. | f(2)>e-4032 |
7.容量为20的样本数据,分组后的频数如下表:
则样本数据落在区间[40,70)的频率为( )
| 分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
| A. | 0.35 | B. | 0.45 | C. | 0.55 | D. | 0.65 |
2.sin70°cos10°+cos110°sin10°=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$. 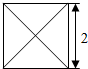 已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.
已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.