题目内容
16.已知在极坐标系与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴,曲线C1:$\left\{\begin{array}{l}{x=cosα}\\{y=sinα}\end{array}\right.$(α为参数),曲线C2:ρ=$\frac{1}{sin(θ+45°)}$;(1)曲线C1,C2是否有公共点,为什么?
(2)将曲线C1向右移动m个单位,使得C1与C2是交于A,B两点,|AB|=$\sqrt{2}$,求m的值.
分析 (1)把曲线C1的参数方程、曲线C2的极坐标方程化为普通方程,利用圆心到直线l的距离d与半径r的关系,
判断曲线C1,C2的公共点数;
(2)曲线C1向右移动m个单位,得到圆的方程,由圆心到直线的距离,求出m的值.
解答 解:(1)把曲线C1的参数方程$\left\{\begin{array}{l}{x=cosα}\\{y=sinα}\end{array}\right.$(α为参数)
化为普通方程是x2+y2=1;
又曲线C2的极坐标方程ρ=$\frac{1}{sin(θ+45°)}$可化为
ρ•($\frac{\sqrt{2}}{2}$sinθ+$\frac{\sqrt{2}}{2}$cosθ)=1,
化为普通方程是$\frac{\sqrt{2}}{2}$y+$\frac{\sqrt{2}}{2}$x=1,
化简得x+y-$\sqrt{2}$=0;
所以圆心O(0,0)到直线l的距离为
d=$\frac{|-\sqrt{2}|}{\sqrt{{1}^{2}{+1}^{2}}}$=1=r,
∴直线l与圆O相切,即曲线C1,C2有一个公共点;
(2)将曲线C1向右移动m个单位,得圆的方程为
(x+m)2+y2=1
C1与C2是交于A,B两点,|AB|=$\sqrt{2}$,
∴圆心(-m,0)到直线x+y-$\sqrt{2}$=0的距离为
d=$\frac{|-m-\sqrt{2}|}{\sqrt{2}}$=$\sqrt{{1}^{2}{-(\frac{\sqrt{2}}{2})}^{2}}$,
解得m=-$\sqrt{2}$±1.
点评 本题考查了直线与圆的应用问题,也考查了参数方程与极坐标的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设x∈R,记不超过x的最大整数为[x],如[2.5]=2,[-2.5]=-3,令{x}=x-[x],则{$\frac{\sqrt{5}+1}{2}$},[$\frac{\sqrt{5}+1}{2}$],$\frac{\sqrt{5}+1}{2}$,三个数构成的数列( )
| A. | 是等比数列但不是等差数列 | B. | 是等差数列但不是等比数列 | ||
| C. | 既是等差数列又是等比数列 | D. | 既不是等差数列也不是等比数列 |
1.函数$y=\frac{ln(2x-1)}{{\sqrt{2-x}}}$的定义域为( )
| A. | ($\frac{1}{2}$,+∞) | B. | ($\frac{1}{2}$,2) | C. | ($\frac{1}{2}$,1) | D. | (-∞,2) |
8.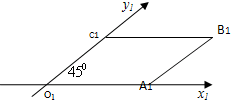 如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )
如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )
 如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )
如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )| A. | 1 | B. | 4 | C. | 1或4 | D. | 不能确定 |
5.若函数f(x)唯一的一个零点同时在区间(0,8)、(0,6)、(0,4)、(0,2)内,那么下列命题中正确的是( )
| A. | 函数f(x)在区间(0,1)内有零点 | B. | 函数f(x)在区间(0,1)或(1,2)内有零点 | ||
| C. | 函数f(x)在区间[2,8)内无零点 | D. | 函数f(x)在区间(1,8)内无零点 |
6.已知等腰三角形的一个底角的正弦值等于$\frac{5}{13}$,则这个等腰三角形的顶角的余弦值为( )
| A. | -$\frac{119}{169}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{119}{169}$ |
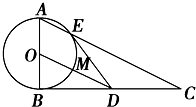 如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.
如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.