题目内容
6.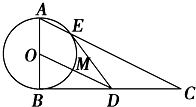 如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.
如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.(1)求证:O、B、D、E四点共圆;
(2)求证:D是BC的中点;
(3)求证:2DE2=DM•AC+DM•AB.
分析 (1)连接BE、OE,由DE为圆O的切线,证出∠OED=∠OBD=90°,利用圆内接四边形形的判定定理得到O、B、D、E四点共圆;
(2)证明:DB=DE=DC,可得D是BC的中点;
(3)延长DO交圆O于点H,由DE为圆O的切线,从而得出DE2=DM•DH,再将DH分解为DO+OH,并利用OH=$\frac{1}{2}$AB和DO=$\frac{1}{2}$AC,化简即可得到等式2DE2=DM•AC+DM•AB成立.
解答  证明:(1)如图,连结OE、BE,则
证明:(1)如图,连结OE、BE,则
∵DE为圆O的切线,∴OE⊥DE
∴∠OBD=∠OED=90°.
∴O、B、D、E四点共圆.…(5分)
(2)∵DE为圆O的切线,DB为圆O的切线,∴DE=DB
∵三角形BEC是直角三角形
∴DB=DE=DC
即D是BC的中点 …(8分)
(3)延长DO交圆O于点H,
∵DE⊥OE,OE是半径,∴DE为圆O的切线.
可得DE2=DM•DH=DM•(DO+OH)=DM•DO+DM•OH.
∵OH=$\frac{1}{2}$AB,OD为△ABC的中位线,得DO=$\frac{1}{2}$AC,
∴DE2=DM•($\frac{1}{2}$AC)+DM•($\frac{1}{2}$AB),
化简得2DE2=DM•AC+DM•AB …(12分)
点评 本题着重考查了圆的切线的性质定理与判定、直径所对的圆周角、全等三角形的判定与性质等知识,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
16.直线x+2y+1=0被圆(x-2)2+(y-1)2=25所截得的弦长为( )
| A. | 5$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | $2\sqrt{5}$ |
18.若(3x-1)7=a7x7+a6x6+…+a1x+a0,则a1+a3+a5+a7=( )
| A. | 26-213 | B. | 26+213 | C. | 27-214 | D. | 27+214 |
15.在圆x2+y2-4x-4y-2=0内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
| A. | 5$\sqrt{2}$ | B. | 10$\sqrt{2}$ | C. | 15$\sqrt{2}$ | D. | 20$\sqrt{2}$ |
 如图,△ABC为直角三角形,∠ABC=90°,以AB为直径的圆交AC与点E,点D是BC边的中点,连接OD交圆于点M,求证:
如图,△ABC为直角三角形,∠ABC=90°,以AB为直径的圆交AC与点E,点D是BC边的中点,连接OD交圆于点M,求证: