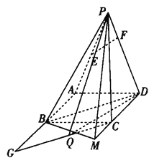
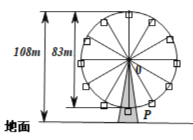
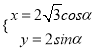题目内容
【题目】已知二次函数![]() ,有两个零点为
,有两个零点为![]() 和
和![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)证明:![]() ;
;
(3)用单调性定义证明函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(4)求![]() 在区间
在区间![]() 上的最小值
上的最小值![]() .
.
【答案】(1)![]() ,
,![]() ;(2)证明见解析;(3)证明见解析;(4)
;(2)证明见解析;(3)证明见解析;(4)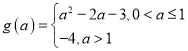 .
.
【解析】
(1)利用韦达定理可得出关于实数![]() 、
、![]() 的方程组,即可求出这两个未知数的值;
的方程组,即可求出这两个未知数的值;
(2)直接计算![]() 和f1x,可证明出
和f1x,可证明出![]() ;
;
(3)任取![]() ,作差
,作差![]() ,因式分解后判断差值的符号,即可证明出函数
,因式分解后判断差值的符号,即可证明出函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(4)分![]() 和
和![]() 两种情况讨论,分析函数
两种情况讨论,分析函数![]() 在区间
在区间![]() 上的单调性,即可得出函数
上的单调性,即可得出函数![]() 在区间
在区间![]() 上的最小值
上的最小值![]() 的表达式.
的表达式.
(1)由韦达定理得![]() ,解得
,解得![]() ;
;
(2)由(1)知![]() ,
,
![]() ,
,![]() ,
,
因此,![]() ;
;
(3)任取![]() ,则
,则![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,
因此,函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(4)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上为减函数,此时
上为减函数,此时![]() ;
;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上减函数,在区间
上减函数,在区间![]() 上为增函数,
上为增函数,
此时![]() .
.
综上所述,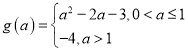 .
.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目