题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:平面![]() 面
面![]() ;
;
(Ⅱ)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
【答案】(I)详见解析;(II)![]() .
.
【解析】
(Ⅰ)由题意得到![]() 面
面![]() ,从而
,从而![]() .又由题意证得四边形
.又由题意证得四边形![]() 为菱形,故得
为菱形,故得![]() ,于是
,于是![]() 平面
平面![]() .根据面面垂直的判定定理可得结论成立.(Ⅱ)由题意得
.根据面面垂直的判定定理可得结论成立.(Ⅱ)由题意得![]() 为
为![]() 中点,建立空间直角坐标系,求出平面
中点,建立空间直角坐标系,求出平面![]() 和平面
和平面![]() 的法向量,根据两向量夹角的余弦值可得二面角的余弦值.
的法向量,根据两向量夹角的余弦值可得二面角的余弦值.
(Ⅰ)证明:因为![]() ,则
,则![]() ,
,
又侧面![]() 底面
底面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 面
面![]() .
.
因为![]() 平面
平面![]() ,则
,则![]() .
.
又因为![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,
则![]() ,又
,又![]()
则![]() 为等边三角形,则四边形
为等边三角形,则四边形![]() 为菱形,
为菱形,
所以![]() .
.
又![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 面
面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅱ)由平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,则
分成体积相等的两部分,则![]() 为
为![]() 中点.
中点.
由(Ⅰ)知![]() 面
面![]() ,且四边形
,且四边形![]() 为菱形、
为菱形、![]() .以A为原点建立如图所示的空间直角坐标系
.以A为原点建立如图所示的空间直角坐标系![]() ,
,

则![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,得
,得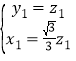 ,
,
令![]() ,可得
,可得![]() .
.
同理,平面![]() 的法向量
的法向量![]() .
.
所以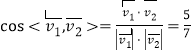 .
.
由图形得二面角![]() 为钝角,
为钝角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】在“应用![]() ”的用户中随机抽取了100名用户进行调查得到如下数据:
”的用户中随机抽取了100名用户进行调查得到如下数据:
每周使用时间 |
|
|
|
|
|
|
男 | 4 | 3 | 3 | 7 | 6 | 30 |
女 | 6 | 5 | 4 | 4 | 8 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)在每周使用该“应用![]() ”时间不超过
”时间不超过![]() 的样本中,按性别分层抽样,随机抽取5名用户:
的样本中,按性别分层抽样,随机抽取5名用户:
①求抽取的5名用户中男,女用户各多少人;
②从这5名用户中随机抽取2名用户,求抽取的2名用户均为男用户的概率.
(2)如果每周使用该“应用![]() ”超过
”超过![]() 的用户认为“喜欢该应用”,能否在犯错误的概率不超过0.05的前提下认为“喜欢该应用”与性别有关.
的用户认为“喜欢该应用”,能否在犯错误的概率不超过0.05的前提下认为“喜欢该应用”与性别有关.
参考公式: ,其中
,其中![]()
下面的临界值表仅供参考:
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |





