题目内容
11.已知f(x)是定义在R上的奇函数,且在(-∞,0]上是增函数,若f(a-2)>-f(a),则实数a的取值范围是( )| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,1) | D. | (1,+∞) |
分析 根据函数奇偶性和单调性之间的关系解不等式即可.
解答 解:∵f(x)是定义在R上的奇函数,且在(-∞,0]上是增函数,
∴f(x)在(-∞,+∞)上为增函数,
若f(a-2)>-f(a).
f(a-2)>f(-a).
则a-2>-a,
即a>1,
故选:D
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系判断函数f(x)的单调性是解决本题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
19.已知复数z=$\frac{a+4i}{1+ai}$,a>0,且z=$\overline{z}$,若1+ai是关于x的方程x2+bx+c=0的一根,则b,c分别为( )
| A. | 4,-8 | B. | 2,-5 | C. | -4,8 | D. | -2,5 |
6.已知集合A={0,1},则满足X⊆A的非空集合X的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.4名优秀学生全部保送到3所学校去,每所学校至少去一名学生,则不同的保送方案有( )
| A. | 12种 | B. | 72种 | C. | 18种 | D. | 36种 |
1.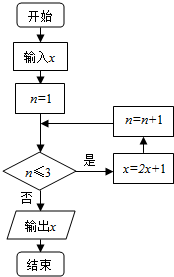 已知实数x∈[1,9],执行如图所示的程序框图,则输出的x不小于55的概率为( )
已知实数x∈[1,9],执行如图所示的程序框图,则输出的x不小于55的概率为( )
 已知实数x∈[1,9],执行如图所示的程序框图,则输出的x不小于55的概率为( )
已知实数x∈[1,9],执行如图所示的程序框图,则输出的x不小于55的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |