题目内容
1.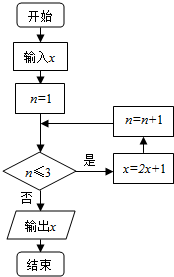 已知实数x∈[1,9],执行如图所示的程序框图,则输出的x不小于55的概率为( )
已知实数x∈[1,9],执行如图所示的程序框图,则输出的x不小于55的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
分析 根据程序框图进行模拟计算,令输出值大于等于55得到输入值的范围,利用几何概型的概率公式求出输出的x不小于55的概率.
解答 解:设实数x∈[1,9],
经过第一次循环得到x=2x+1,n=2
经过第二循环得到x=2(2x+1)+1,n=3
经过第三次循环得到x=2[2(2x+1)+1]+1,n=3此时输出x
输出的值为8x+7
令8x+7≥55,得x≥6
由几何概型得到输出的x不小于55的概率为=$\frac{9-6}{9-1}$=$\frac{3}{8}$.
故选:C
点评 解决程序框图中的循环结构时,一般采用先根据框图的流程写出前几次循环的结果,进行模拟计算是解决本题的关键.

练习册系列答案
相关题目
11.已知f(x)是定义在R上的奇函数,且在(-∞,0]上是增函数,若f(a-2)>-f(a),则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,1) | D. | (1,+∞) |
12.已知集合M={x|x2-2x-3≤0},N={x|-2<x<2},则M∩N=( )
| A. | ∅ | B. | {x|-1≤x<2} | C. | {x|-2≤x<-1} | D. | {x|2≤x<3} |
6.下列结论正确的是( )
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一实数λ使$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B. | “若θ=$\frac{π}{3}$,则cosθ=$\frac{1}{2}$”的否命题为“若θ≠$\frac{π}{3}$,则cosθ≠$\frac{1}{2}$” | |
| C. | 已知向量$\overrightarrow{a}$、$\overrightarrow{b}$为非零向量,则“$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为钝角”的充要条件是“$\overrightarrow{a}$$•\overrightarrow{b}$<0” | |
| D. | 若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1>0 |
13.已知命题p:“?x∈R,ex>0”,命题q:“?x0∈R,x0-2>x02”,则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
12.已知平面α,β的法向量分别是(-2,3,m),(4,λ,0),若α∥β,则λ+m的值( )
| A. | 8 | B. | 6 | C. | -10 | D. | -6 |