题目内容
1.已知向量$\overrightarrow a$=(-cos(π-θ),sin(-θ)),$\overrightarrow b$=([cos($\frac{π}{4}$-$\frac{θ}{2}$)+sin($\frac{π}{4}$-$\frac{θ}{2}$)][cos($\frac{π}{4}$-$\frac{θ}{2}$)-sin($\frac{π}{4}$-$\frac{θ}{2}$)],2cos2$\frac{θ}{2}$-1).(1)求证:$\overrightarrow a$⊥$\overrightarrow b$
(2)设$\overrightarrow x$=$\overrightarrow a$+(t2+3)$\overrightarrow b$,$\overrightarrow y$=-k$\overrightarrow a$+t$\overrightarrow b$,g(t)=$\frac{{k+λ{t^2}}}{t}$(λ∈[-8,0]),若存在不等于0的实数k和t(t∈[1,2]),满足$\overrightarrow x$⊥$\overrightarrow y$,试求g(t)的最小值h(λ),并求出h(λ)的最小值.
分析 (1)首先化简两个向量的坐标,然后进行数量积的运算;
(2)由$\overrightarrow x⊥\overrightarrow y$可得$\overrightarrow x•\overrightarrow y=0$,进一步利用k,t表示,化简后根据解析式特点,讨论最小值的取得.
解答 解:(1)$\overrightarrow a$=(-cos(π-θ),sin(-θ))=(cosθ,-sinθ)
$\overrightarrow b$=([cos($\frac{π}{4}$-$\frac{θ}{2}$)+sin($\frac{π}{4}$-$\frac{θ}{2}$)][cos($\frac{π}{4}$-$\frac{θ}{2}$)-sin($\frac{π}{4}$-$\frac{θ}{2}$)],2cos2$\frac{θ}{2}$-1)=(sinθ,cosθ)
所以$\overrightarrow a•\overrightarrow b$=sinθcosθ-sinθcosθ=0,
∴$\overrightarrow a⊥\overrightarrow b$; (3分)
(2)由$\overrightarrow x⊥\overrightarrow y$可得$\overrightarrow x•\overrightarrow y=0$,
即$[{\overrightarrow a+({{t^2}+3})\overrightarrow b}]•({-k\overrightarrow a+t\overrightarrow b})=0$,
∴$-k{\overrightarrow a^2}+({{t^3}+3t}){\overrightarrow b^2}+[{t-k({{t^2}+3})}]\overrightarrow a•\overrightarrow b=0$,
∴$-k{|{\overrightarrow a}|^2}+({{t^3}+3t}){|{\overrightarrow b}|^2}=0$,
又∵${|{\overrightarrow a}|^2}=1,{|{\overrightarrow b}|^2}=1$,
∴-k+t3+t=0,∴k=t3+3t,(5分)
∴g(t)=$\frac{{k+λ{t^2}}}{t}=\frac{{{t^3}+λ{t^2}+3t}}{t}={t^2}+λt+3={({t+\frac{λ}{2}})^2}+3-\frac{λ^2}{4}$,(t∈[1,2])(7分)
①当$-\frac{λ}{2}<1$即λ>-2时,g(t)min=g(1)=λ+4
②当$1≤-\frac{λ}{2}≤2$即-4≤λ≤-2时,$g{(t)_{min}}=g({-\frac{λ}{2}})=3-\frac{λ^2}{4}$
③当$-\frac{λ}{2}>2$即λ<-4时,g(t)min=g(2)=2λ+7
∴$h(λ)=g{(t)_{min}}=\left\{\begin{array}{l}2λ+7,({-8≤λ<-4})\\ 3-\frac{λ^2}{4},({-4≤λ≤-2})\\ λ+4,({-2<λ≤0})\end{array}\right.$(10分)
∴h(λ)min=-9(12分)
点评 本题考查了利用三角函数的诱导公式以及逆用两角和与差的三角函数公式化简三角函数式、平面向量的数量积公式的运用以及讨论思想的考查;属于中档题.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{13}{16}$ | D. | $\frac{3}{16}$ |
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | 16 | B. | 16$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,1) | D. | (1,+∞) |
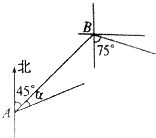 中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.
中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.