题目内容
2.已知函数f(x)=2sin(2x+$\frac{π}{3}$)+1;(1)求函数f(x)的单调递增区间;
(2)若存在区间[a,b](a,b∈R且a<b),使得y=f(x)在[a,b]上至少含有6个零点,在满足上述条件的[a,b]中,求b-a的最小值.
分析 (1)由条件利用正弦函数的单调性求得函数f(x)的单调递增区间.
(2)令f(x)=0,求出 x的值,可得相邻的零点之间的间隔依次为$\frac{π}{3}$、$\frac{2π}{3}$.f(x)在[a,b]上至少含有6个零点,等价于b-a的最小值为2×$\frac{2π}{3}$+3×$\frac{π}{3}$.
解答 解:(1)对于函数f(x)=2sin(2x+$\frac{π}{3}$)+1,令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈z,
求得kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,可得函数的增区间为[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$],k∈z.
(2)令f(x)=0,求出 sin(2x+$\frac{π}{3}$)=-$\frac{1}{2}$,∴x=kπ-$\frac{π}{4}$,或x=kπ-$\frac{7π}{12}$,
故相邻的零点之间的间隔依次为$\frac{π}{3}$、$\frac{2π}{3}$.
y=f(x)在[a,b]上至少含有6个零点,等价于b-a的最小值为 2×$\frac{2π}{3}$+3×$\frac{π}{3}$=$\frac{7π}{3}$.
点评 本题主要考查正弦函数的图象,正弦函数的单调性和零点,属于基础题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
13.sin45°cos15°-cos135°sin165°=( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
10.在△ABC中,角A,B,C所对的边分别为a,b,c,A=60°,b=2,△ABC的面积为4$\sqrt{3}$,则边c的值为( )
| A. | 16 | B. | 16$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
7.若点P在曲线y=-$\frac{2}{3}$x3-2x2-x+3上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
| A. | [$\frac{π}{4}$,$\frac{π}{2}$) | B. | [$\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,π) | C. | [0,$\frac{π}{3}$]∪($\frac{2π}{3}$,π) | D. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,π) |
14.函数f(x)=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}(2x-3)}}$的定义域为( )
| A. | ($\frac{3}{2}$,+∞) | B. | (2,+∞) | C. | (0,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,2) |
11.已知f(x)是定义在R上的奇函数,且在(-∞,0]上是增函数,若f(a-2)>-f(a),则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,1) | D. | (1,+∞) |
12.已知集合M={x|x2-2x-3≤0},N={x|-2<x<2},则M∩N=( )
| A. | ∅ | B. | {x|-1≤x<2} | C. | {x|-2≤x<-1} | D. | {x|2≤x<3} |
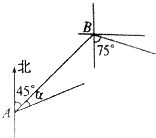 中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.
中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.