题目内容
20.现定义max{a,b}=$\left\{\begin{array}{l}{a,a≥b}\\{b,a<b}\end{array}$,若y,z>0且M=max{$\frac{\sqrt{y}}{\sqrt{(1-x)z}}$,$\frac{\sqrt{z}}{\sqrt{(3+x)y}}$},则M的最小值是$\frac{\sqrt{2}}{2}$.分析 根据二次函数的图象和性质,可得$\frac{\sqrt{y}}{\sqrt{(1-x)z}}•\frac{\sqrt{z}}{\sqrt{(3+x)y}}$≥$\frac{1}{2}$,当且仅当x=-1时,取得最小值,故$\frac{\sqrt{y}}{\sqrt{(1-x)z}}$,$\frac{\sqrt{z}}{\sqrt{(3+x)y}}$不可能都小于$\frac{\sqrt{2}}{2}$,进而得到M的最小值.
解答 解:$\frac{\sqrt{y}}{\sqrt{(1-x)z}}•\frac{\sqrt{z}}{\sqrt{(3+x)y}}$=$\frac{1}{\sqrt{(1-x)(3+x)}}$=$\frac{1}{\sqrt{-{x}^{2}-2x+3}}$=$\frac{1}{\sqrt{-({x+1)}^{2}+4}}$≥$\frac{1}{2}$,
当且仅当x=-1时,取得最小值,
故$\frac{\sqrt{y}}{\sqrt{(1-x)z}}$,$\frac{\sqrt{z}}{\sqrt{(3+x)y}}$不可能都小于$\frac{\sqrt{2}}{2}$,
即$\frac{\sqrt{y}}{\sqrt{(1-x)z}}$,$\frac{\sqrt{z}}{\sqrt{(3+x)y}}$至少有一个大于等于或等于$\frac{\sqrt{2}}{2}$,
故当$\frac{\sqrt{y}}{\sqrt{(1-x)z}}$=$\frac{\sqrt{z}}{\sqrt{(3+x)y}}$=$\frac{\sqrt{2}}{2}$时,M取得最小值,
故答案为:$\frac{\sqrt{2}}{2}$
点评 本题考查的知识点是函数的最值及其几何意义,其中分析两式的积$\frac{\sqrt{y}}{\sqrt{(1-x)z}}•\frac{\sqrt{z}}{\sqrt{(3+x)y}}$≥$\frac{1}{2}$,并正确理解其意义,是解答的关键.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $m=\frac{π}{6},M=\frac{π}{3}$ | B. | $m=\frac{π}{3},M=\frac{2π}{3}$ | C. | $m=\frac{4π}{3},M=2π$ | D. | $m=\frac{2π}{3},M=\frac{4π}{3}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}i$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
| A. | $\frac{2}{e}$ | B. | 1 | C. | 2 | D. | e |
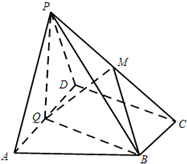 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.