题目内容
10.已知函数y=ex,若f(x)的图象的一条切线经过点(-1,0),则这条切线与直线x=1及x轴所围成的三角形面积为( )| A. | $\frac{2}{e}$ | B. | 1 | C. | 2 | D. | e |
分析 设出切点坐标求解切线方程,然后求解三角形的面积.
解答 解:函数y=ex,若f(x)的图象的一条切线经过点(-1,0),设切点(a,ea),
则y′=ex,在切点(a,ea),处的切线斜率为:ea,
由题意可得:ea=$\frac{{e}^{a}-0}{a+1}$,解得a=0,切线向量为:1,切点为(0,1),
切线方程为:y=x+1.
切线与直线x=1及x轴所围成的三角形面积为:$\frac{1}{2}×2×2=2$.
故选:C.
点评 本题考查切线方程的求法,三角形的面积的求法,求解切线的斜率是解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
5.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )
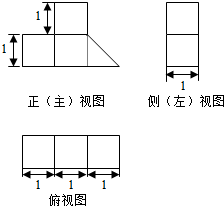

| A. | $\frac{7}{3}$ m3 | B. | $\frac{9}{2}$ m3 | C. | $\frac{9}{4}$ m3 | D. | $\frac{7}{2}$ m3 |
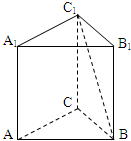 如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.
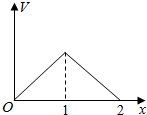
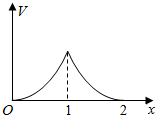
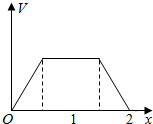
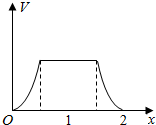
如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.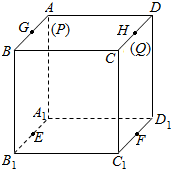 在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )