题目内容
15.定义在区间[a,b](b>a)上的函数$f(x)=\frac{1}{2}sinx-\frac{{\sqrt{3}}}{2}cosx$的值域是$[-\frac{1}{2},1]$,则b-a的最大值M和最小值m分别是( )| A. | $m=\frac{π}{6},M=\frac{π}{3}$ | B. | $m=\frac{π}{3},M=\frac{2π}{3}$ | C. | $m=\frac{4π}{3},M=2π$ | D. | $m=\frac{2π}{3},M=\frac{4π}{3}$ |
分析 利用两角差的正弦化简得,f(x)=sin($x-\frac{π}{3}$),由函数f(x)在$[a-\frac{π}{3},b-\frac{π}{3}]$上的值域为$[-\frac{1}{2},1]$,不妨设$a-\frac{π}{3}=-\frac{π}{6}$,可得b-$\frac{π}{3}$∈[$\frac{π}{2},\frac{7}{6}π$],由此可得b-a的最大值M和最小值m的值.
解答 解:$f(x)=\frac{1}{2}sinx-\frac{{\sqrt{3}}}{2}cosx$=sin($x-\frac{π}{3}$),
∵x∈[a,b](b>a),∴$x-\frac{π}{3}∈[a-\frac{π}{3},b-\frac{π}{3}]$,
由函数f(x)在$[a-\frac{π}{3},b-\frac{π}{3}]$上的值域为$[-\frac{1}{2},1]$,
不妨设$a-\frac{π}{3}=-\frac{π}{6}$,则b-$\frac{π}{3}$∈[$\frac{π}{2},\frac{7}{6}π$],
∴b-a的最大值M=$\frac{7}{6}π-(-\frac{π}{6})=\frac{4π}{3}$;
最小值m=$\frac{π}{2}-(-\frac{π}{6})=\frac{2π}{3}$.
故选:D.
点评 本题考查两角差的正弦,考查了三角函数的值是基础题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
8.运行如图的程序框图,若输入n=2015,则输出的a=( )
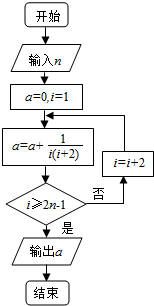

| A. | $\frac{2015}{4031}$ | B. | $\frac{4030}{4031}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{2015}{4029}$ |
7.若二项式(2-x)n(n∈N*)的展开式中所有项的系数的绝对值之和是a,所有项的二项式系数之和是b,则$\frac{b}{a}+\frac{a}{b}$的最小值是( )
| A. | 2 | B. | $\frac{13}{6}$ | C. | $\frac{7}{3}$ | D. | $\frac{15}{6}$ |
5.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )
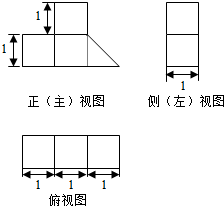

| A. | $\frac{7}{3}$ m3 | B. | $\frac{9}{2}$ m3 | C. | $\frac{9}{4}$ m3 | D. | $\frac{7}{2}$ m3 |
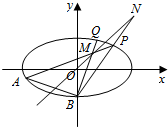 如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.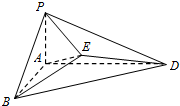
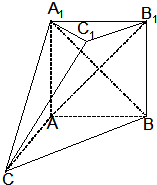 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1