题目内容
已知函数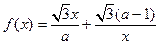 (
(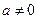 且
且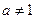 ).
).
(1) 试就实数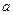 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;
(2) 已知当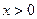 时,函数在
时,函数在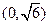 上单调递减,在
上单调递减,在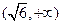 上单调递增,求
上单调递增,求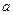 的值并写出函数的解析式;
的值并写出函数的解析式;
(3) (理)记(2)中的函数的图像为曲线 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线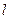 ,使得
,使得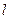 为曲线
为曲线 的对称轴?若存在,求出
的对称轴?若存在,求出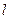 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(文) 记(2)中的函数的图像为曲线 ,试问曲线
,试问曲线 是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
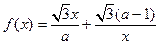 (
(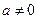 且
且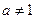 ).
).(1) 试就实数
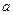 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;(2) 已知当
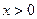 时,函数在
时,函数在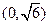 上单调递减,在
上单调递减,在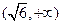 上单调递增,求
上单调递增,求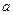 的值并写出函数的解析式;
的值并写出函数的解析式; (3) (理)记(2)中的函数的图像为曲线
 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线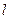 ,使得
,使得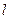 为曲线
为曲线 的对称轴?若存在,求出
的对称轴?若存在,求出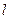 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.(文) 记(2)中的函数的图像为曲线
 ,试问曲线
,试问曲线 是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.(1) ①当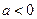 时,函数
时,函数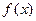 的单调递增区间为
的单调递增区间为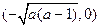 及
及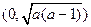 ,
,
②当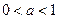 时,函数
时,函数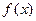 的单调递增区间为
的单调递增区间为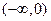 及
及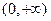 ,
,
③当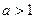 时,函数
时,函数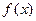 的单调递增区间为
的单调递增区间为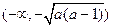 及
及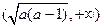 .
.
(2)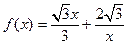
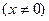 .
.
(3) (理)存在直线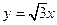 及
及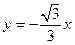 为曲线
为曲线 的对称轴.
的对称轴.
(文)函数为奇函数,曲线 为中心对称图形.
为中心对称图形.
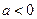 时,函数
时,函数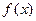 的单调递增区间为
的单调递增区间为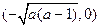 及
及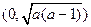 ,
, ②当
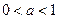 时,函数
时,函数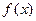 的单调递增区间为
的单调递增区间为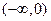 及
及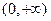 ,
,③当
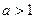 时,函数
时,函数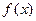 的单调递增区间为
的单调递增区间为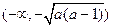 及
及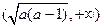 .
.(2)
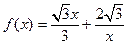
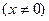 .
. (3) (理)存在直线
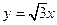 及
及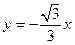 为曲线
为曲线 的对称轴.
的对称轴. (文)函数为奇函数,曲线
 为中心对称图形.
为中心对称图形.(1) ①当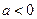 时,函数
时,函数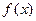 的单调递增区间为
的单调递增区间为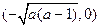 及
及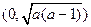 ,
,
②当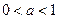 时,函数
时,函数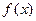 的单调递增区间为
的单调递增区间为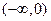 及
及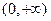 ,
,
③当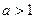 时,函数
时,函数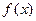 的单调递增区间为
的单调递增区间为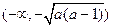 及
及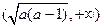 .
.
(6分)
(2) 由题设及(1)中③知 且
且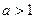 ,解得
,解得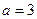 , (9分)
, (9分)
因此函数解析式为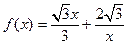
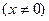 . (10分)
. (10分)
(3) (理)假设存在经过原点的直线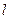 为曲线
为曲线 的对称轴,显然
的对称轴,显然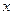 、
、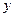 轴不是曲线
轴不是曲线 的对称轴,故可设
的对称轴,故可设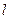 :
: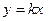 (
(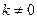 ),
),
设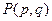 为曲线
为曲线 上的任意一点,
上的任意一点,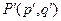 与
与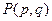 关于直线
关于直线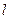 对称,且
对称,且
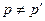 ,
,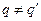 ,则
,则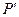 也在曲线
也在曲线 上,由此得
上,由此得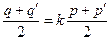 ,
,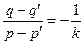 ,
,
且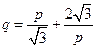 ,
,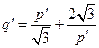 , (14分)
, (14分)
整理得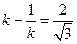 ,解得
,解得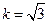 或
或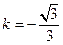 ,
,
所以存在直线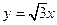 及
及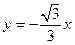 为曲线
为曲线 的对称轴. (16分)
的对称轴. (16分)
(文)该函数的定义域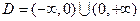 ,曲线
,曲线 的对称中心为
的对称中心为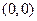 ,
,
因为对任意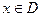 ,
,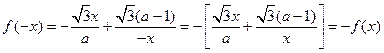 ,
,
所以该函数为奇函数,曲线 为中心对称图形.
为中心对称图形.
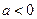 时,函数
时,函数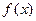 的单调递增区间为
的单调递增区间为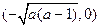 及
及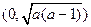 ,
, ②当
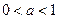 时,函数
时,函数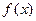 的单调递增区间为
的单调递增区间为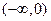 及
及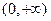 ,
,③当
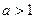 时,函数
时,函数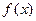 的单调递增区间为
的单调递增区间为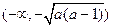 及
及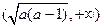 .
.(6分)
(2) 由题设及(1)中③知
 且
且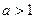 ,解得
,解得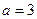 , (9分)
, (9分)因此函数解析式为
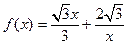
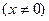 . (10分)
. (10分)(3) (理)假设存在经过原点的直线
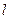 为曲线
为曲线 的对称轴,显然
的对称轴,显然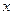 、
、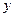 轴不是曲线
轴不是曲线 的对称轴,故可设
的对称轴,故可设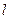 :
: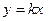 (
(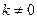 ),
),设
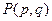 为曲线
为曲线 上的任意一点,
上的任意一点,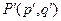 与
与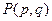 关于直线
关于直线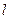 对称,且
对称,且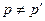 ,
,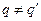 ,则
,则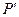 也在曲线
也在曲线 上,由此得
上,由此得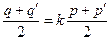 ,
,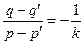 ,
,且
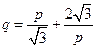 ,
,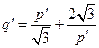 , (14分)
, (14分)整理得
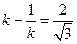 ,解得
,解得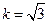 或
或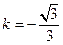 ,
,所以存在直线
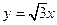 及
及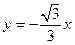 为曲线
为曲线 的对称轴. (16分)
的对称轴. (16分)(文)该函数的定义域
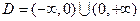 ,曲线
,曲线 的对称中心为
的对称中心为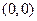 ,
,因为对任意
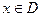 ,
,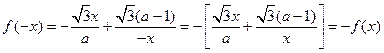 ,
,所以该函数为奇函数,曲线
 为中心对称图形.
为中心对称图形.
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
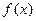 满足
满足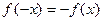 ,函数
,函数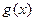 满足
满足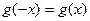 ,且对任意
,且对任意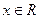 有
有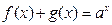 (
(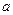 >0,且
>0,且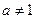 )
)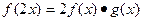 ;
;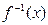 ,当
,当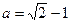 时,试比较
时,试比较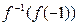 与
与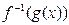 的大小
的大小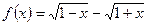 .
.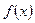 的奇偶性;
的奇偶性;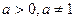 ,解关于
,解关于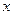 不等式:
不等式: 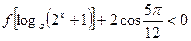 .
.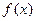 的定义域为R,对任意的
的定义域为R,对任意的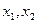 都满足
都满足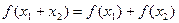 ,当
,当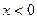 时,
时,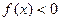 .
.
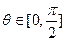 时,使不等式
时,使不等式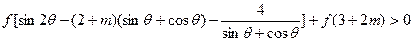
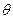 恒成立,如存在,求出m的取值范围;若不存在,说明理由.
恒成立,如存在,求出m的取值范围;若不存在,说明理由. 件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
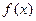
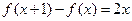
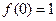
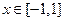 时,不等式:
时,不等式: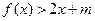 恒成立,求实数
恒成立,求实数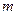 的范围.
的范围.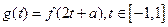
 ,求
,求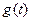 的最大值;
的最大值;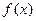 是定义在
是定义在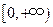 的函数,满足
的函数,满足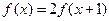 .设
.设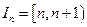 ,
,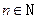 .当
.当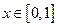 时,
时,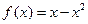 .分别求当
.分别求当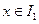 、
、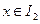 、
、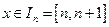 时,
时,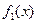 、
、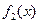 、
、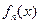 .
.