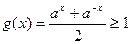题目内容
已知函数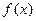 满足
满足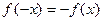 ,函数
,函数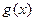 满足
满足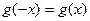 ,且对任意
,且对任意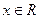 有
有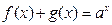 (
(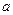 >0,且
>0,且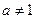 )
)
(1)求证: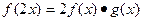 ;
;
(2)设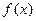 的反函数为
的反函数为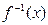 ,当
,当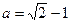 时,试比较
时,试比较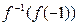 与
与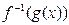 的大小
的大小
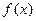 满足
满足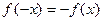 ,函数
,函数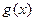 满足
满足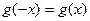 ,且对任意
,且对任意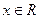 有
有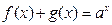 (
(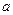 >0,且
>0,且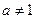 )
)(1)求证:
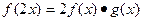 ;
;(2)设
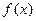 的反函数为
的反函数为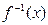 ,当
,当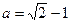 时,试比较
时,试比较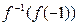 与
与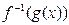 的大小
的大小(1)见解析(2)

 ①
①


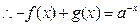 ② 由①②得
② 由①②得 ,
, 
(1) 由前易证结论成立
(2) 当
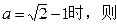 0<
0<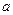 <1,
<1, 是
是 上的减函数,所以
上的减函数,所以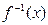 也是减函数,又
也是减函数,又 ,
,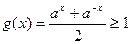


练习册系列答案
相关题目
题目内容
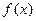 满足
满足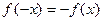 ,函数
,函数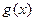 满足
满足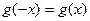 ,且对任意
,且对任意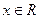 有
有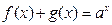 (
(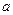 >0,且
>0,且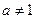 )
)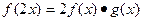 ;
;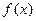 的反函数为
的反函数为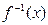 ,当
,当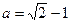 时,试比较
时,试比较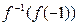 与
与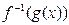 的大小
的大小
 ①
①


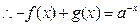 ② 由①②得
② 由①②得 ,
, 
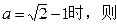 0<
0<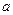 <1,
<1, 是
是 上的减函数,所以
上的减函数,所以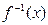 也是减函数,又
也是减函数,又 ,
,