题目内容

(Ⅰ)将日利润y(元)表示成日产量x(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值
(Ⅰ)y=-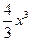 +3600x(x∈N*,1≤x≤40)(Ⅱ)日产量为30件时最大值为72000元
+3600x(x∈N*,1≤x≤40)(Ⅱ)日产量为30件时最大值为72000元
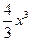 +3600x(x∈N*,1≤x≤40)(Ⅱ)日产量为30件时最大值为72000元
+3600x(x∈N*,1≤x≤40)(Ⅱ)日产量为30件时最大值为72000元(I)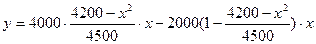 .………………4分
.………………4分
=3600x-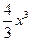
∴所求的函数关系是y=-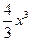 +3600x(x∈N*,1≤x≤40).………………6分
+3600x(x∈N*,1≤x≤40).………………6分
(II)显然y′=3600-4x.令y′=0,解得x=30.
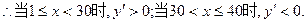
∴函数y=-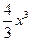 +3600x(x∈N*,1≤x≤40)在
+3600x(x∈N*,1≤x≤40)在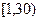 上是单调递增函数,
上是单调递增函数,
在 上是单调递减函数. …………………………9分
上是单调递减函数. …………………………9分
∴当x=30时,函数y=-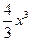 +3600x(x∈N*,1≤x≤40)取最大值,最大值为
+3600x(x∈N*,1≤x≤40)取最大值,最大值为
-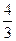 ×303+3600×30=72000(元).
×303+3600×30=72000(元).
∴该厂的日产量为30件时,日利润最大,其最大值为72000元.…………12分
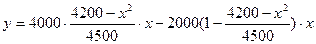 .………………4分
.………………4分=3600x-
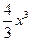
∴所求的函数关系是y=-
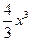 +3600x(x∈N*,1≤x≤40).………………6分
+3600x(x∈N*,1≤x≤40).………………6分(II)显然y′=3600-4x.令y′=0,解得x=30.
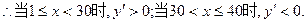
∴函数y=-
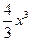 +3600x(x∈N*,1≤x≤40)在
+3600x(x∈N*,1≤x≤40)在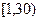 上是单调递增函数,
上是单调递增函数,在
 上是单调递减函数. …………………………9分
上是单调递减函数. …………………………9分∴当x=30时,函数y=-
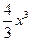 +3600x(x∈N*,1≤x≤40)取最大值,最大值为
+3600x(x∈N*,1≤x≤40)取最大值,最大值为-
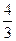 ×303+3600×30=72000(元).
×303+3600×30=72000(元).∴该厂的日产量为30件时,日利润最大,其最大值为72000元.…………12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
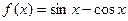 ,
,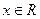 .(1)求函数
.(1)求函数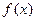 在
在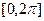 内的单调递增区间;
内的单调递增区间;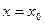 处取到最大值,求
处取到最大值,求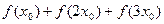 的值;
的值;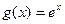 (
(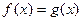 在
在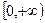 内没有实数解.(参考数据:
内没有实数解.(参考数据: ,
,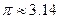 )
)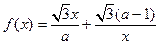 (
(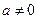 且
且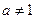 ).
).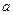 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;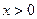 时,函数在
时,函数在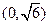 上单调递减,在
上单调递减,在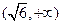 上单调递增,求
上单调递增,求 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线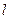 ,使得
,使得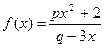 是奇函数,且
是奇函数,且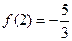 .
.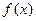 的解析式;
的解析式; 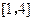 上的最小值
上的最小值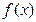 不是常数函数,对于
不是常数函数,对于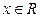 有
有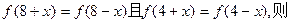
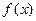 的周期是 .
的周期是 .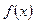 的定义域为
的定义域为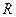 ,对任意实数
,对任意实数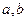 满足
满足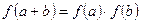 .
. ,试求
,试求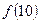 ;(2)设当
;(2)设当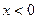 时,
时,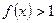 ,试解不等式
,试解不等式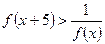 .
.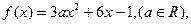 若
若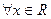 ,不等式
,不等式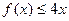 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.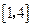 上的函数
上的函数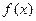 是减函数,求满足不等式
是减函数,求满足不等式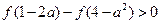
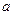 的集合.
的集合.