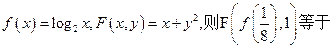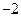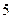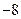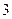题目内容
已知函数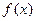 的定义域为R,对任意的
的定义域为R,对任意的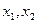 都满足
都满足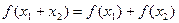 ,当
,当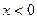 时,
时,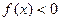 .
.
(1)判断并证明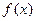 的单调性和奇偶性;
的单调性和奇偶性;
(2)是否存在这样的实数m,当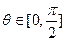 时,使不等式
时,使不等式
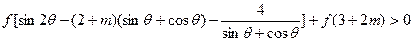
对所有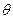 恒成立,如存在,求出m的取值范围;若不存在,说明理由.
恒成立,如存在,求出m的取值范围;若不存在,说明理由.
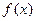 的定义域为R,对任意的
的定义域为R,对任意的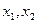 都满足
都满足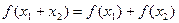 ,当
,当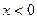 时,
时,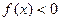 .
.
(1)判断并证明
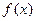 的单调性和奇偶性;
的单调性和奇偶性; (2)是否存在这样的实数m,当
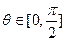 时,使不等式
时,使不等式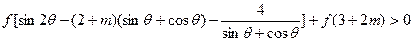
对所有
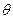 恒成立,如存在,求出m的取值范围;若不存在,说明理由.
恒成立,如存在,求出m的取值范围;若不存在,说明理由.(1) 为奇函数,
为奇函数,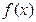 是增函数 (2)
是增函数 (2)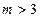 时,原命题成立.
时,原命题成立.
 为奇函数,
为奇函数,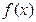 是增函数 (2)
是增函数 (2)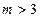 时,原命题成立.
时,原命题成立.(1)令

有
 即
即 为奇函数
为奇函数在R上任取
 ,由题意知
,由题意知
则
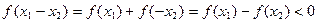
故
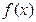 是增函数
是增函数 (2)要使
 ,只须
,只须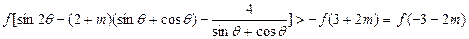
又由
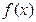 为单调增函数有
为单调增函数有
 令
令
原命题等价于
 恒成立
恒成立
令
 上为减函数,
上为减函数,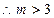 时,原命题成立.
时,原命题成立.
练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
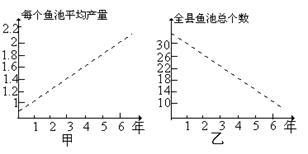
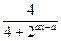 在[0,1]上的最小值为
在[0,1]上的最小值为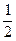 ,
,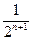 (n∈N
(n∈N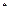 )
)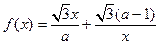 (
(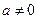 且
且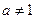 ).
).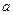 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;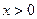 时,函数在
时,函数在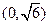 上单调递减,在
上单调递减,在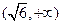 上单调递增,求
上单调递增,求 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线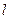 ,使得
,使得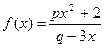 是奇函数,且
是奇函数,且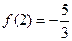 .
.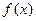 的解析式;
的解析式; 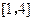 上的最小值
上的最小值 的一条直线与函数
的一条直线与函数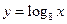 的图象交于
的图象交于 ,
,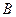 两点,分别过点
两点,分别过点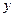 轴的平行线与函数
轴的平行线与函数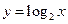 的图象交于
的图象交于 ,
,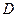 两点.
两点.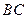 平行于
平行于 轴时,求点
轴时,求点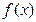 不是常数函数,对于
不是常数函数,对于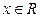 有
有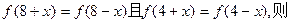
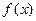 的周期是 .
的周期是 .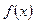 的定义域为
的定义域为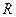 ,对任意实数
,对任意实数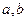 满足
满足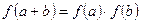 .
. ,试求
,试求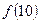 ;(2)设当
;(2)设当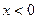 时,
时,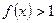 ,试解不等式
,试解不等式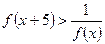 .
.