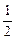题目内容
已知函数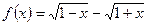 .
.
(1)判断函数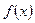 的奇偶性;
的奇偶性;
(2)判断函数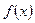 在定义域内是增函数还是减函数?请说明理由;
在定义域内是增函数还是减函数?请说明理由;
(3)已知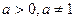 ,解关于
,解关于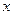 不等式:
不等式: 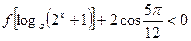 .
.
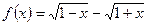 .
.(1)判断函数
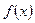 的奇偶性;
的奇偶性;(2)判断函数
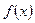 在定义域内是增函数还是减函数?请说明理由;
在定义域内是增函数还是减函数?请说明理由;(3)已知
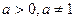 ,解关于
,解关于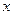 不等式:
不等式: 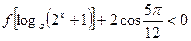 .
. (1)函数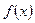 是奇函数;(2)函数
是奇函数;(2)函数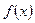 在定义域
在定义域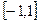 上是单调减函数.;
上是单调减函数.;
(3)故当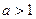 时,解集为
时,解集为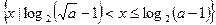 ;当
;当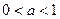 时,解集为空集。
时,解集为空集。
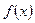 是奇函数;(2)函数
是奇函数;(2)函数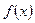 在定义域
在定义域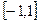 上是单调减函数.;
上是单调减函数.;(3)故当
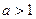 时,解集为
时,解集为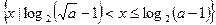 ;当
;当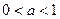 时,解集为空集。
时,解集为空集。(1)由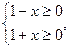 得函数
得函数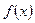 的定义域是
的定义域是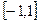 . 又
. 又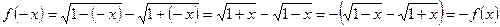 .
.
所以函数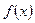 是奇函数.
是奇函数.
(2)设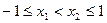 ,则
,则
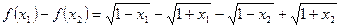
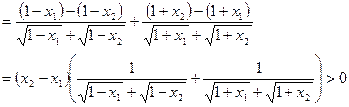
所以函数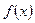 在定义域
在定义域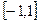 上是单调减函数.
上是单调减函数.
注:也可以用导数知识判断.
(3)因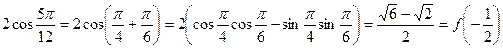 ,所以,不等式等价为
,所以,不等式等价为
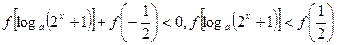 ,
,
考虑到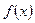 在定义域
在定义域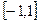 上是单调减函数,所以又化为
上是单调减函数,所以又化为
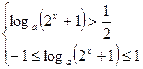 ,即
,即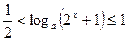 ,
,
当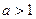 时,
时,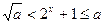 ,即
,即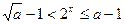 ,
,
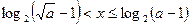 ;
;
当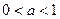 时,
时,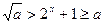 ,即
,即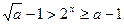 ,这与
,这与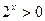 矛盾.
矛盾.
故当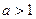 时,解集为
时,解集为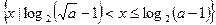 ;
;
当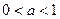 时,解集为空集.
时,解集为空集.
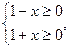 得函数
得函数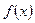 的定义域是
的定义域是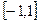 . 又
. 又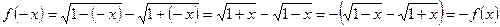 .
.所以函数
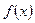 是奇函数.
是奇函数. (2)设
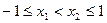 ,则
,则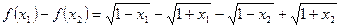
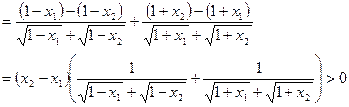
所以函数
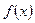 在定义域
在定义域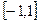 上是单调减函数.
上是单调减函数.注:也可以用导数知识判断.
(3)因
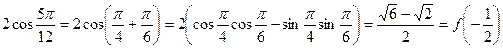 ,所以,不等式等价为
,所以,不等式等价为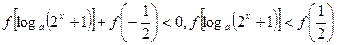 ,
,考虑到
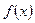 在定义域
在定义域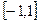 上是单调减函数,所以又化为
上是单调减函数,所以又化为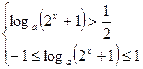 ,即
,即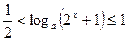 ,
, 当
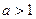 时,
时,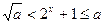 ,即
,即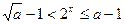 ,
,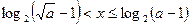 ;
;当
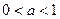 时,
时,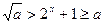 ,即
,即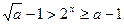 ,这与
,这与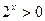 矛盾.
矛盾.故当
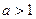 时,解集为
时,解集为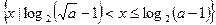 ;
;当
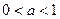 时,解集为空集.
时,解集为空集.
练习册系列答案
相关题目
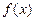 是定义在
是定义在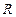 上的偶函数,当
上的偶函数,当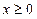 时,
时,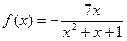 .
.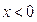 时
时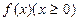 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;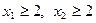 且
且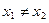 ,证明:
,证明: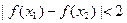 .
.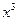 -ax在[1,+∞)上是单调函数.
-ax在[1,+∞)上是单调函数. ≥1,f(x)≥1,且f(f(
≥1,f(x)≥1,且f(f(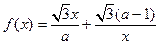 (
(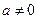 且
且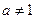 ).
).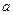 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;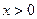 时,函数在
时,函数在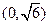 上单调递减,在
上单调递减,在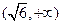 上单调递增,求
上单调递增,求 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线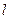 ,使得
,使得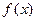 与产量
与产量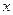 之间的关系式为
之间的关系式为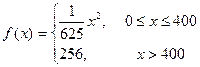 ,每件产品的售价
,每件产品的售价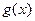 与产量
与产量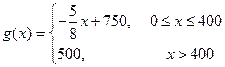 .
. 与产量
与产量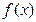 不是常数函数,对于
不是常数函数,对于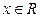 有
有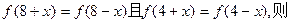
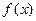 的周期是 .
的周期是 .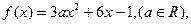 若
若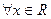 ,不等式
,不等式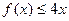 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.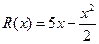 (万元)
(万元)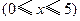 ,其中
,其中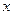 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).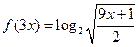 ,则
,则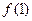 的值为( )
的值为( )