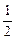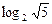题目内容
某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元,该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元,假设商店每月购进这种商品m件,且当月销完,你估计哪个月份盈利最大?
估计6月份盈利最大
设出厂价波动函数为y1=6+Asin(ω1x+φ1)
易知A=2 T1=8 ω1=
 +φ1=
+φ1=
 φ1=-
φ1=- ∴y1=6+2sin(
∴y1=6+2sin( x-
x- )
)
设销售价波动函数为y2=8+Bsin(ω2x+φ2)
易知B=2 T2=8 ω2=
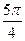 +φ2=
+φ2=
 φ2=-
φ2=-
∴y2=8+2sin( x-
x- )
)
每件盈利 y=y2-y1=[8+2sin( x-
x- )]-[6+2sin(
)]-[6+2sin( x-
x- )]
)]
=2-2 sin
sin x
x
当sin x=-1
x=-1
 x=2kπ-
x=2kπ-
 x=8k-2时y取最大值
x=8k-2时y取最大值
当k=1 即x=6时 y最大 ∴估计6月份盈利最大
易知A=2 T1=8 ω1=

 +φ1=
+φ1=
 φ1=-
φ1=- ∴y1=6+2sin(
∴y1=6+2sin( x-
x- )
)设销售价波动函数为y2=8+Bsin(ω2x+φ2)
易知B=2 T2=8 ω2=

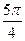 +φ2=
+φ2=
 φ2=-
φ2=-
∴y2=8+2sin(
 x-
x- )
)每件盈利 y=y2-y1=[8+2sin(
 x-
x- )]-[6+2sin(
)]-[6+2sin( x-
x- )]
)]=2-2
 sin
sin x
x当sin
 x=-1
x=-1
 x=2kπ-
x=2kπ-
 x=8k-2时y取最大值
x=8k-2时y取最大值当k=1 即x=6时 y最大 ∴估计6月份盈利最大

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
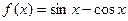 ,
,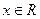 .(1)求函数
.(1)求函数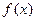 在
在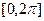 内的单调递增区间;
内的单调递增区间;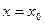 处取到最大值,求
处取到最大值,求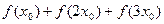 的值;
的值;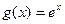 (
(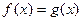 在
在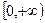 内没有实数解.(参考数据:
内没有实数解.(参考数据: ,
,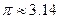 )
)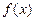 是定义在
是定义在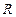 上的偶函数,当
上的偶函数,当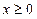 时,
时,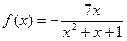 .
.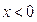 时
时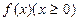 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;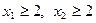 且
且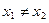 ,证明:
,证明: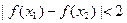 .
.
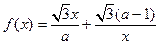 (
(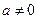 且
且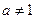 ).
).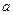 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;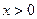 时,函数在
时,函数在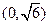 上单调递减,在
上单调递减,在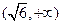 上单调递增,求
上单调递增,求 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线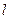 ,使得
,使得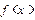 是定义在
是定义在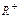 上的减函数,并且满足
上的减函数,并且满足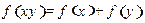 ,
,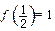 .
.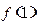 的值;
的值;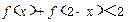 .
.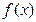 不是常数函数,对于
不是常数函数,对于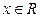 有
有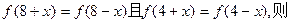
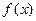 的周期是 .
的周期是 .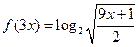 ,则
,则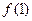 的值为( )
的值为( )