题目内容
(本小题满分12分)设 和
和 是函数
是函数 的两个极值点。
的两个极值点。
(Ⅰ)求 和
和 的值;(Ⅱ)求
的值;(Ⅱ)求 的单调区间
的单调区间
 和
和 是函数
是函数 的两个极值点。
的两个极值点。(Ⅰ)求
 和
和 的值;(Ⅱ)求
的值;(Ⅱ)求 的单调区间
的单调区间(Ⅰ)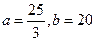 (Ⅱ)单调增区间是
(Ⅱ)单调增区间是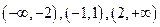 单调减区间是
单调减区间是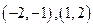
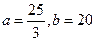 (Ⅱ)单调增区间是
(Ⅱ)单调增区间是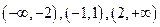 单调减区间是
单调减区间是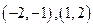
(Ⅰ)因为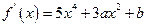 由假设知:
由假设知: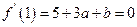
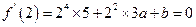 解得
解得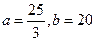
(Ⅱ)由(Ⅰ)知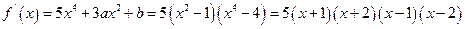
当 时,
时,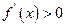 当
当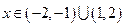 时,
时,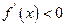
因此 的单调增区间是
的单调增区间是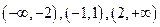
 的单调减区间是
的单调减区间是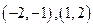
【点评】:此题重点考察利用导数研究函数的极值点,单调性,最值问题;
【突破】:熟悉函数的求导公式,理解函数极值与导数、函数单调性与导数的关系;重视图象或示意图的辅助作用。
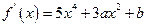 由假设知:
由假设知: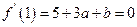
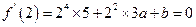 解得
解得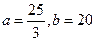
(Ⅱ)由(Ⅰ)知
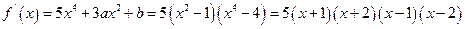
当
 时,
时,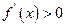 当
当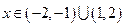 时,
时,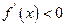
因此
 的单调增区间是
的单调增区间是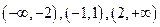
 的单调减区间是
的单调减区间是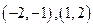
【点评】:此题重点考察利用导数研究函数的极值点,单调性,最值问题;
【突破】:熟悉函数的求导公式,理解函数极值与导数、函数单调性与导数的关系;重视图象或示意图的辅助作用。

练习册系列答案
相关题目
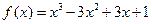 的反函数是
的反函数是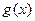 ,则
,则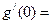 ___________.
___________.
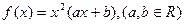 在
在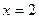 时有极值,其图象在点
时有极值,其图象在点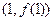 处的切线与直线
处的切线与直线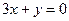 平行.(1)求
平行.(1)求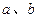 的值和函数
的值和函数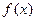 的单调区间;(2)若当
的单调区间;(2)若当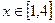 时,恒有
时,恒有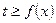 ,试确定
,试确定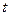 的取值范围.
的取值范围.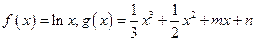 ,直线
,直线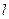 与函数
与函数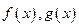 的图象都相切于点
的图象都相切于点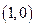 。
。 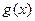 的解析式;
的解析式;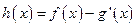 (其中
(其中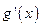 是
是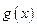 的导函数),求函数
的导函数),求函数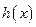 的极大值.
的极大值.