题目内容
已知函数f(x)=x3+ax2+bx+a2在x=1处取得极值10，则a+b=＿＿＿＿＿
-7
由函数在x=1处取得极值10，得：
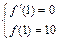，即
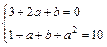，解得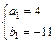
，
，
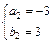将a1=4,b1=-11代入，有f(x)=x3+4x2-11x+16,f′(x)=3x2+8x-11=(x-1)3x+11)，
可以得出x=1时有极小值10.将a2=-3,b2=3代入，有f(x)=x3-3x2+3x+9,f′(x)=3x2-6x+3=3(x-1)2≥0
故对当x∈R，f(x)为增函数，∴此时，x=1不是极值点，∴a=4,b=-11,故a+b=-7
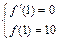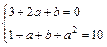，即，解得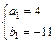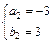，，将a1=4,b1=-11代入，有f(x)=x3+4x2-11x+16,f′(x)=3x2+8x-11=(x-1)3x+11)，
可以得出x=1时有极小值10.将a2=-3,b2=3代入，有f(x)=x3-3x2+3x+9,f′(x)=3x2-6x+3=3(x-1)2≥0
故对当x∈R，f(x)为增函数，∴此时，x=1不是极值点，∴a=4,b=-11,故a+b=-7
练习册系列答案
全能练考卷系列答案
相关题目
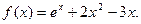（I）求曲线
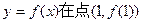处的切线方程； （Ⅱ）求证函数
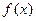在区间[0，1]上存在唯一的极值点，并用二分法求函数取得极值时相应x的近似值（误差不超过0.2）；（参考数据e≈2.7，
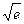≈1.6，e0.3≈1.3）
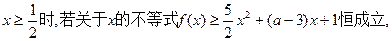试求实数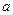
的取值范围。
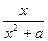(a>0)在[1，+∞）上的最大值为
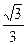,则a的值为 
,
.
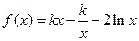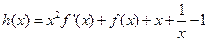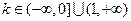时,函数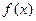
在其定义域内为单调函数;(II)若函数
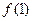)处的切线斜率为0,且当
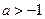时,
≥
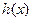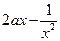在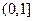
上恒成立,求实数a的取值范围.
．
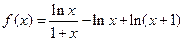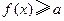的解集为（0，+
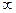）？若存在，求a的取值范围；若不存在，试说明理由．
和
是函数
的两个极值点。
和
的值；（Ⅱ）求
的单调区间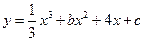
（c为实常数）上任意一点为切点的切线的斜率恒为非负数，则实数b的取值范围为 。
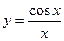的导数是（ ）
