题目内容
已知f1（x）=sinx-cosx，fn+1（x）是fn（x）的导函数，即f2（x）=f1′（x），f3（x）=f2′（x），…，fn+1（x）=fn′（x），n∈N*，则f2012（x）=（ ）
| A．sinx+cosx | B．sinx-cosx | C．-sinx+cosx | D．-sinx-cosx |
∵f1（x）=sinx-cosx，∴f2(x)=f1′(x)=cosx+sinx，f3(x)=f2′(x)=-sinx+cosx，f4(x)=f3′(x)=-cosx-sinx，f5(x)=f4′(x)=sinx-cosx．
∴f5（x）=f1（x），fn+4k（x）=fn（x）．
∴f2012（x）=f502×4+4（x）=f4（x）=-cosx-sinx．
故选D．
∴f5（x）=f1（x），fn+4k（x）=fn（x）．
∴f2012（x）=f502×4+4（x）=f4（x）=-cosx-sinx．
故选D．
练习册系列答案
相关题目
已知函数
，
，
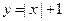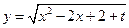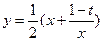
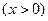的最小值恰好是方程
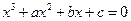的三个根，其中
．
；
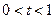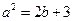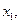
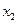是函数
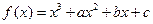的两个极值点．若
，
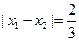的解析式．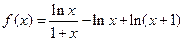
．
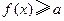的解集为（0，+
）？若存在，求a的取值范围；若不存在，试说明理由．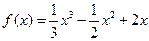
，
，
，
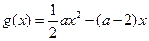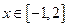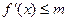恒成立，求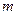
的最小值；
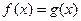在区间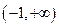
有三个不同的实根，求
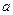的取值范围．
和
是函数
的两个极值点。
和
的值；（Ⅱ）求
的单调区间
