题目内容

函数f（x）为偶函数，且f′（x）存在，则f′（多）=（　　）
A．1B．-1C．0D．-x
因为f（x）为偶函数，则f（x）=f（-x），
所以f'（x）=f'（-x）（-1），
右边移到左边，得f'（x）+f'（-x）=0，
取x=0得：f'（0）+f'（0）=0
即f'（0）=0．
故选C．
练习册系列答案
相关题目
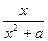若函数 f(x)=(a>0)在[1，+∞）上的最大值为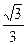,则a的值为        
（本小题满分12分）设和是函数的两个极值点。
（Ⅰ）求和的值；（Ⅱ）求的单调区间
定义在R上的函数f（x）满足f（4）=1，f′（x）为f（x）的导函数，已知函数y=f′（x）的图象如图所示．若正数a，b满足f（2a+b）＜1，则
a+2
b+2
的取值范围是（　　）
A．（
1
3
，2）		B．（-∞，
1
2
）∪（3，+∞）		C．（
1
2
，3）		D．（-∞，3）
y=sin（3-4x），则y′=（　　）
A．-sin（3-4x）B．3-cos（-4x）C．4cos（3-4x）D．-4cos（3-4x）
已知在R上可导的函数f（x）的图象如图所示，则不等式f（x）•f′（x）＜0的解集为（　　）
A．（-2，0）B．（-∞，-2）∪（-1，0）C．（-∞，-2）∪（0，+∞）D．（-2，-1）∪（0，+∞）
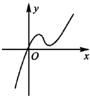
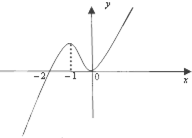
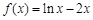函数的单调递减区间是         .
已知f（x）=x2+1，则f′（0）的值是（　　）
A．2B．-2C．0D．2x
函数y=2sinx的导数y′=（　　）
A．2cosxB．-2cosxC．cosxD．-cosx

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网