题目内容
如图,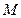 是抛物线上
是抛物线上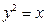 上的一点,动弦
上的一点,动弦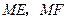 分别交
分别交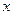 轴于
轴于 两点,且
两点,且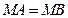 .
.
(1) 若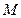 为定点,证明:直线
为定点,证明:直线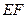 的斜率为定值;
的斜率为定值;
(2) 若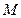 为动点,且
为动点,且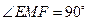 ,求
,求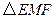 的重心
的重心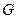 的轨迹方程.
的轨迹方程.
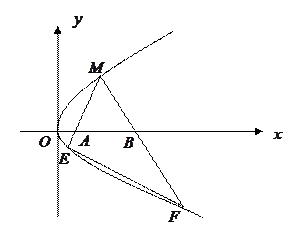
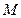 是抛物线上
是抛物线上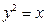 上的一点,动弦
上的一点,动弦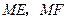 分别交
分别交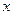 轴于
轴于 两点,且
两点,且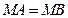 .
.(1) 若
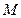 为定点,证明:直线
为定点,证明:直线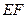 的斜率为定值;
的斜率为定值;(2) 若
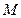 为动点,且
为动点,且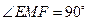 ,求
,求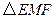 的重心
的重心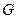 的轨迹方程.
的轨迹方程.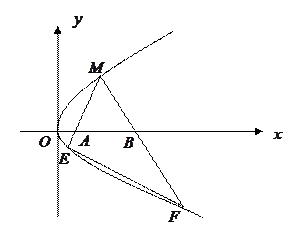
(1)证明见答案 (2)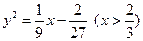
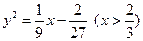
(1)设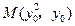 ,直线
,直线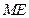 的斜率为
的斜率为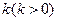 ,则直线
,则直线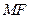 的斜率为
的斜率为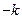 ,
,
 直线
直线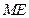 的方程为
的方程为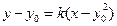 .
.
由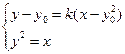 消
消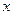 得
得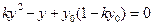 .
.
解得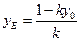 ,
,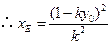 .
.
同理可得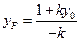 ,
,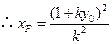 .
.
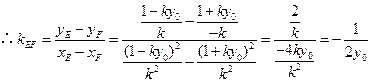 (定值).
(定值).
所以直线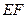 的斜率为定值.
的斜率为定值.
(2)当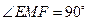 时,
时,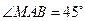 ,所以
,所以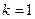 ,
,
 直线
直线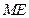 的方程为:
的方程为: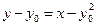 ,
,
由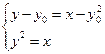 得
得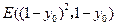 ,同理可得
,同理可得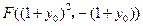 .
.
设得心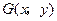 ,
,
则有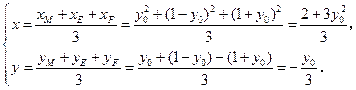
消去参数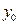 得
得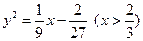 .
.
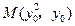 ,直线
,直线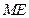 的斜率为
的斜率为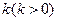 ,则直线
,则直线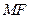 的斜率为
的斜率为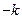 ,
, 直线
直线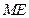 的方程为
的方程为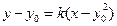 .
.由
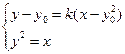 消
消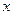 得
得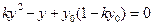 .
.解得
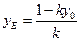 ,
,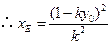 .
.同理可得
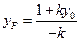 ,
,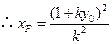 .
.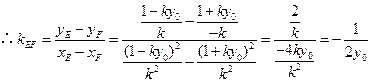 (定值).
(定值).所以直线
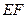 的斜率为定值.
的斜率为定值.(2)当
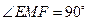 时,
时,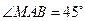 ,所以
,所以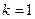 ,
, 直线
直线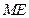 的方程为:
的方程为: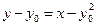 ,
,由
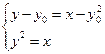 得
得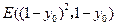 ,同理可得
,同理可得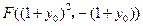 .
.设得心
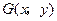 ,
,则有
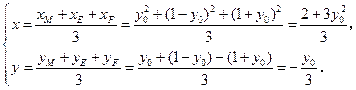
消去参数
 得
得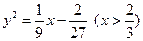 .
.
练习册系列答案
相关题目
 过点A,且与抛物线C 相切,直线
过点A,且与抛物线C 相切,直线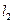 :x=a(a≠-1)交抛物线C于B,交直线
:x=a(a≠-1)交抛物线C于B,交直线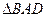 的面积为S1,求
的面积为S1,求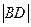 及S1的值.
及S1的值.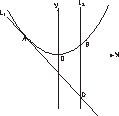
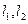 所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.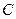 经过定点
经过定点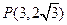 ,它的一个焦点为
,它的一个焦点为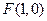 ,对应于该焦点的
,对应于该焦点的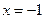 ,斜率为
,斜率为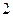 的直线
的直线 交圆锥曲线
交圆锥曲线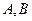 两点,且
两点,且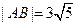 ,
,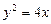 的焦点作一条斜率为k(k≠0)的弦,此弦满足:①弦长不超过8;②弦所在的直线与椭圆3x2+ 2y2= 2相交,求k的取值范围.
的焦点作一条斜率为k(k≠0)的弦,此弦满足:①弦长不超过8;②弦所在的直线与椭圆3x2+ 2y2= 2相交,求k的取值范围.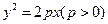 的焦点作倾斜角为
的焦点作倾斜角为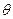 的直线
的直线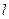 ,设
,设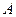 ,
,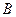 两点,求
两点,求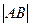 .
.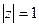 , 则点Q(x+y,xy)的轨迹是 ( ).
, 则点Q(x+y,xy)的轨迹是 ( ). 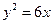 的准线方程为_____.
的准线方程为_____.