题目内容
抛物线y2=2px的焦点弦AB的中点为M,A、B、M在准线上的
影依次为C、D、N.求证:
(1)A、O、D三点共线,B、O、C三点共线;
(2)FN⊥AB(F为抛物线的焦点)
影依次为C、D、N.求证:
(1)A、O、D三点共线,B、O、C三点共线;
(2)FN⊥AB(F为抛物线的焦点)
(1)设A(x1,y1)、B(x2,y2)、中点M(x0,y0),焦点F的坐标是(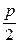 ,0).
,0).
由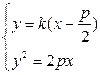 得ky2-2py-kp2=0.
得ky2-2py-kp2=0.
∴A、B、M在准线上的射影依次为C、D、N,
∴C(-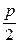 ,y1)、D(-
,y1)、D(-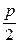 ,y2)、N(-
,y2)、N(-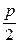 ,y0).
,y0).
∵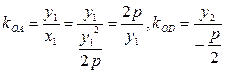 ,
,
由ky2-2py-kp2=0
得y1y2=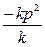 =-p2,
=-p2,
∴kOA=kOD,∴A、O、D三点共线.同理可证B、O、C三点共线.
(2)kFN=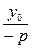 ,当x1=x2时,显然FN⊥AB;当x1≠x2时,
,当x1=x2时,显然FN⊥AB;当x1≠x2时,
kAB=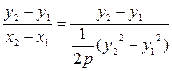
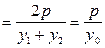 ,∴kFN·kAB=-1.∴FN⊥AB.综上所述知FN⊥AB成立.
,∴kFN·kAB=-1.∴FN⊥AB.综上所述知FN⊥AB成立.
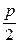 ,0).
,0).由
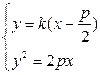 得ky2-2py-kp2=0.
得ky2-2py-kp2=0.∴A、B、M在准线上的射影依次为C、D、N,
∴C(-
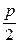 ,y1)、D(-
,y1)、D(-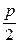 ,y2)、N(-
,y2)、N(-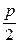 ,y0).
,y0).∵
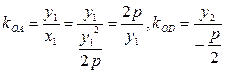 ,
,由ky2-2py-kp2=0
得y1y2=
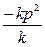 =-p2,
=-p2,∴kOA=kOD,∴A、O、D三点共线.同理可证B、O、C三点共线.
(2)kFN=
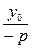 ,当x1=x2时,显然FN⊥AB;当x1≠x2时,
,当x1=x2时,显然FN⊥AB;当x1≠x2时,kAB=
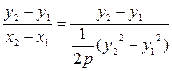
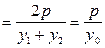 ,∴kFN·kAB=-1.∴FN⊥AB.综上所述知FN⊥AB成立.
,∴kFN·kAB=-1.∴FN⊥AB.综上所述知FN⊥AB成立.同答案

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
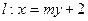 交抛物线y2=4x于A、B两点.
交抛物线y2=4x于A、B两点.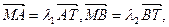 当m变化时,求
当m变化时,求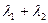 的值;
的值;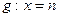 上的射影为D、E,连结AE、BD相交于一点N,则当m变化时,点N为定点的充要条件是n=-2.
上的射影为D、E,连结AE、BD相交于一点N,则当m变化时,点N为定点的充要条件是n=-2.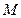 是抛物线上
是抛物线上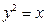 上的一点,动弦
上的一点,动弦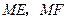 分别交
分别交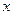 轴于
轴于 两点,且
两点,且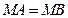 .
.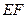 的斜率为定值;
的斜率为定值;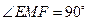 ,求
,求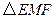 的重心
的重心 的轨迹方程.
的轨迹方程.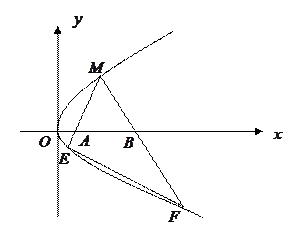
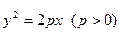 ,焦点为F,一直线
,焦点为F,一直线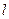 与抛物线交于A、B两点,且
与抛物线交于A、B两点,且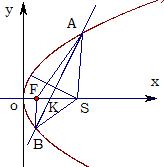
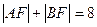 ,且AB的垂直平分线恒过定点S(6, 0)
,且AB的垂直平分线恒过定点S(6, 0)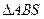 面积的最大值.
面积的最大值.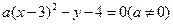 按向量
按向量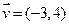 平移后所得抛物线的焦点坐标为___________.
平移后所得抛物线的焦点坐标为___________.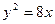 只有一个公共点的直线有 ( )
只有一个公共点的直线有 ( )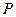 在抛物线
在抛物线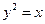 上,点
上,点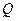 在圆
在圆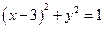 上,求
上,求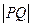 的最小值。
的最小值。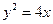 的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于
的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于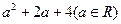 ,则这样的直线( )
,则这样的直线( )