题目内容
设抛物线的顶点在原点,准线方程为x=-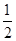 .
.
(1)求抛物线的标准方程;
(2)若点P是抛物线上的动点,点P在y轴上的射影是Q,点M ,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
(3)过抛物线焦点F作互相垂直的两直线分别交抛物线于A,C,B,D,求四边形ABCD面积的最小值.
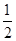 .
.(1)求抛物线的标准方程;
(2)若点P是抛物线上的动点,点P在y轴上的射影是Q,点M
 ,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;(3)过抛物线焦点F作互相垂直的两直线分别交抛物线于A,C,B,D,求四边形ABCD面积的最小值.
(1)y2=2x.(2)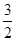 (3)8.
(3)8.
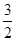 (3)8.
(3)8.(1) 由题意知以直线l:x=-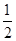 为准线的抛物线,得
为准线的抛物线,得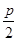 =
=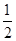 ,∴p=1,方程为y2=2x.
,∴p=1,方程为y2=2x.
(2)易知点M在抛物线的外侧,延长PQ交直线x=-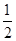 于点N,
于点N,
由抛物线的定义可知|PN|=|PQ|+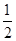 =|PF|,
=|PF|,
当三点M,P,F共线时,|PM|+|PF|最小,此时为|PM|+|PF|=|MF|.
又焦点坐标为F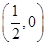 ,所以|MF|=
,所以|MF|=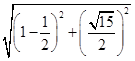 =2,
=2,
即|PM|+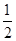 +|PQ|的最小值为2,所以|PM|+|PQ|的最小值为
+|PQ|的最小值为2,所以|PM|+|PQ|的最小值为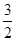 .
.
(3)设过F的直线方程为y=k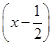 ,A(x1,y1),C(x2,y2),
,A(x1,y1),C(x2,y2),
由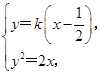 得k2x2-(k2+2)x+
得k2x2-(k2+2)x+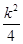 =0,
=0,
由韦达定理得x1+x2=1+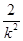 ,x1x2=
,x1x2=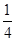 ,
,
所以|AC|=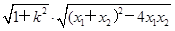 =2+
=2+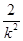 ,
,
同理|BD|=2+2k2.
所以四边形ABCD的面积S=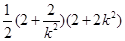 =2
=2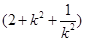 ≥8,
≥8,
即四边形ABCD面积的最小值为8.
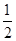 为准线的抛物线,得
为准线的抛物线,得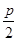 =
=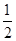 ,∴p=1,方程为y2=2x.
,∴p=1,方程为y2=2x.(2)易知点M在抛物线的外侧,延长PQ交直线x=-
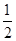 于点N,
于点N,由抛物线的定义可知|PN|=|PQ|+
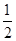 =|PF|,
=|PF|,当三点M,P,F共线时,|PM|+|PF|最小,此时为|PM|+|PF|=|MF|.
又焦点坐标为F
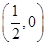 ,所以|MF|=
,所以|MF|=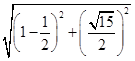 =2,
=2,即|PM|+
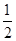 +|PQ|的最小值为2,所以|PM|+|PQ|的最小值为
+|PQ|的最小值为2,所以|PM|+|PQ|的最小值为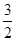 .
.(3)设过F的直线方程为y=k
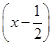 ,A(x1,y1),C(x2,y2),
,A(x1,y1),C(x2,y2),由
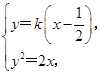 得k2x2-(k2+2)x+
得k2x2-(k2+2)x+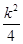 =0,
=0, 由韦达定理得x1+x2=1+
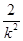 ,x1x2=
,x1x2=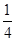 ,
,所以|AC|=
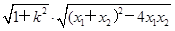 =2+
=2+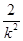 ,
,同理|BD|=2+2k2.
所以四边形ABCD的面积S=
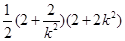 =2
=2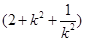 ≥8,
≥8,即四边形ABCD面积的最小值为8.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目

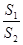 =λ,求λ的取值范围.
=λ,求λ的取值范围.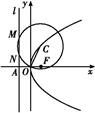
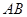 为抛物线
为抛物线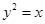 上的动弦,且
上的动弦,且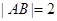 , 则弦
, 则弦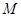 到
到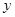 轴的最小距离为
轴的最小距离为 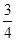
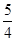
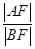 的值等于( ).
的值等于( ).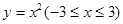 绕
绕 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是 .
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是 .