题目内容
如图X15-3所示,已知圆C1:x2+(y-1)2=4和抛物线C2:y=x2-1,过坐标原点O的直线与C2相交于点A,B,定点M的坐标为(0,-1),直线MA,MB分别与C1相交于点D,E.

(1)求证:MA⊥MB;
(2)记△MAB,△MDE的面积分别为S1,S2,若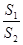 =λ,求λ的取值范围.
=λ,求λ的取值范围.

(1)求证:MA⊥MB;
(2)记△MAB,△MDE的面积分别为S1,S2,若
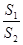 =λ,求λ的取值范围.
=λ,求λ的取值范围.(1)见解析(2)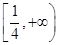
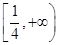
(1)证明:设直线AB的方程为y=kx,A(x1,y1),B(x2,y2),
则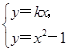 ?x2-kx-1=0,所以x1+x2=k,x1x2=-1.
?x2-kx-1=0,所以x1+x2=k,x1x2=-1.
又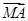 ·
·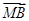 =(x1,y1+1)·(x2,y2+1)=(k2+1)x1x2+k(x1+x2)+1=-k2-1+k2+1=0,
=(x1,y1+1)·(x2,y2+1)=(k2+1)x1x2+k(x1+x2)+1=-k2-1+k2+1=0,
∴MA⊥MB.
(2)设直线MA的方程为y=k1x-1,MB的方程为y=k2x-1,k1k2=-1.
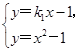 解得
解得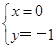 或
或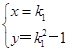
∴A(k1,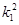 -1),同理可得B(k2,
-1),同理可得B(k2,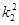 -1),
-1),
∴S1=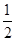 |MA||MB|=
|MA||MB|=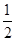
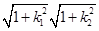 |k1k2|.
|k1k2|.
又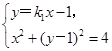 解得
解得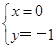 或
或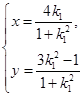
∴D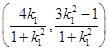 ,同理可得E
,同理可得E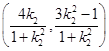 .
.
∴S2=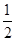 |MD||ME|=
|MD||ME|=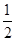
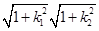
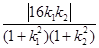 .
.
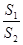 =λ=
=λ=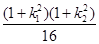 =
= ≥
≥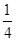 .故λ的取值范围是
.故λ的取值范围是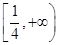 .
.
则
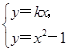 ?x2-kx-1=0,所以x1+x2=k,x1x2=-1.
?x2-kx-1=0,所以x1+x2=k,x1x2=-1. 又
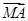 ·
·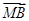 =(x1,y1+1)·(x2,y2+1)=(k2+1)x1x2+k(x1+x2)+1=-k2-1+k2+1=0,
=(x1,y1+1)·(x2,y2+1)=(k2+1)x1x2+k(x1+x2)+1=-k2-1+k2+1=0,∴MA⊥MB.
(2)设直线MA的方程为y=k1x-1,MB的方程为y=k2x-1,k1k2=-1.
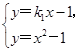 解得
解得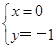 或
或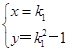
∴A(k1,
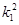 -1),同理可得B(k2,
-1),同理可得B(k2,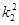 -1),
-1),∴S1=
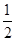 |MA||MB|=
|MA||MB|=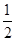
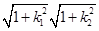 |k1k2|.
|k1k2|.又
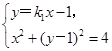 解得
解得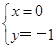 或
或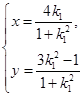
∴D
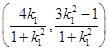 ,同理可得E
,同理可得E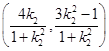 .
.∴S2=
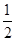 |MD||ME|=
|MD||ME|=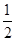
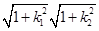
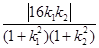 .
.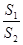 =λ=
=λ=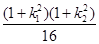 =
= ≥
≥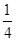 .故λ的取值范围是
.故λ的取值范围是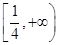 .
.
练习册系列答案
相关题目
 .若存在,请求出点B的坐标;若不存在,请说明理由.
.若存在,请求出点B的坐标;若不存在,请说明理由.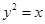 的焦点,A,B是该抛物线上的两点,
的焦点,A,B是该抛物线上的两点,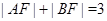 ,则线段AB的中点到y轴的距离为 ( )
,则线段AB的中点到y轴的距离为 ( )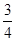
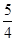
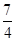
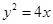 的焦点为
的焦点为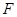 ,准线为
,准线为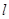 ,经过
,经过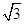 的直线与抛物线在
的直线与抛物线在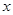 轴上方的部分相交于点
轴上方的部分相交于点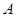 ,
,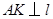 ,垂足为
,垂足为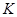 ,则
,则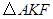 的面积是( )
的面积是( )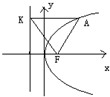

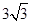
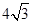

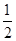 .
. ,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;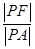 的最小值是( )
的最小值是( )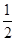
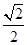

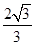

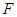 为抛物线
为抛物线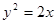 的焦点,
的焦点,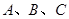 为抛物线上三点,若
为抛物线上三点,若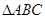 的重心,则
的重心,则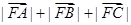 的值为( )
的值为( )