题目内容
设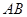 为抛物线
为抛物线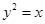 上的动弦,且
上的动弦,且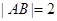 , 则弦
, 则弦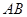 的中点
的中点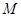 到
到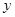 轴的最小距离为
轴的最小距离为
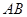 为抛物线
为抛物线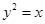 上的动弦,且
上的动弦,且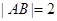 , 则弦
, 则弦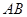 的中点
的中点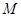 到
到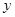 轴的最小距离为
轴的最小距离为 | A.2 | B.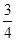 | C.1 | D.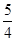 |
B
试题分析:设
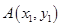 、
、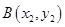 ,弦
,弦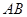 的中点
的中点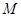 到
到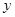 轴的距离最小,则弦
轴的距离最小,则弦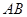 过抛物线的焦点
过抛物线的焦点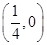 ,由题意得准线为
,由题意得准线为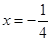 ,∴
,∴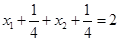 ,即
,即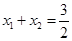 ,∴弦
,∴弦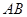 的中点
的中点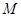 到
到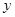 轴的最小距离
轴的最小距离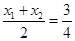 .
.
练习册系列答案
相关题目
题目内容
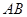 为抛物线
为抛物线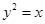 上的动弦,且
上的动弦,且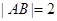 , 则弦
, 则弦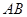 的中点
的中点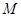 到
到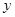 轴的最小距离为
轴的最小距离为 | A.2 | B.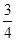 | C.1 | D.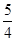 |
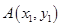 、
、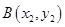 ,弦
,弦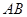 的中点
的中点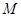 到
到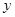 轴的距离最小,则弦
轴的距离最小,则弦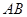 过抛物线的焦点
过抛物线的焦点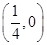 ,由题意得准线为
,由题意得准线为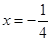 ,∴
,∴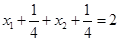 ,即
,即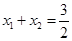 ,∴弦
,∴弦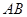 的中点
的中点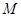 到
到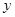 轴的最小距离
轴的最小距离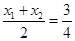 .
.