题目内容
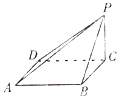
【题目】已知四边形![]() 是矩形,
是矩形,![]() ,将
,将![]() 沿着对角线AC翻折,得到
沿着对角线AC翻折,得到![]() ,设顶点
,设顶点![]() 在平面
在平面![]() 上的投影为O.
上的投影为O.
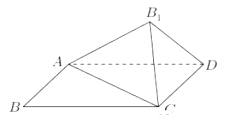
(1)若点O恰好落在边AD上,①求证:![]() 平面
平面![]() ;②若
;②若![]() ,
,![]() ,当BC取到最小值时,求k的值;
,当BC取到最小值时,求k的值;
(2)当![]() 时,若点O恰好落在
时,若点O恰好落在![]() 的内部(不包括边界),求二面角
的内部(不包括边界),求二面角![]() 的余弦值的取值范围.
的余弦值的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 由面面垂直的判定定理得平面
由面面垂直的判定定理得平面![]() 平面ACD,从而
平面ACD,从而![]() ,由线面垂直得
,由线面垂直得![]() ,由矩形性质得
,由矩形性质得![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
![]() 作矩形ABMN,使得
作矩形ABMN,使得![]() 在MN上,设
在MN上,设![]() ,
,![]() ,求出y,利用基本不等式,即可求出当BC取到最小值时,k的值;
,求出y,利用基本不等式,即可求出当BC取到最小值时,k的值;
![]() 作
作![]() ,交AC于E,交AD于F,当点O恰好落在
,交AC于E,交AD于F,当点O恰好落在![]() 的内部
的内部![]() 不包括边界
不包括边界![]() ,点O恰好在线段EF上,
,点O恰好在线段EF上,![]() 为二面角
为二面角![]() 的平面角,由此能求出二面角
的平面角,由此能求出二面角![]() 的余弦值的取值范围.
的余弦值的取值范围.
![]() 证明:
证明:![]() 点
点![]() 在平面ABCD上的射影为O,点O恰好落在边AD上,
在平面ABCD上的射影为O,点O恰好落在边AD上,
![]() 平面
平面![]() 平面ACD,又
平面ACD,又![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,
![]() 平面
平面![]() .
.
![]() 作矩形ADMN,使得
作矩形ADMN,使得![]() 在MN上,
在MN上,
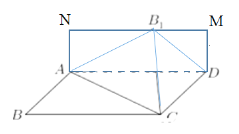
设![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]() ∽
∽![]() ,
,
![]() ,
,
在Rt![]() 中
中
![]() ,
,
当且仅当![]() 时取等号,y有最小值,
时取等号,y有最小值,![]() ;
;
![]() 作
作![]() ,交AC于E,交AD于F,
,交AC于E,交AD于F,
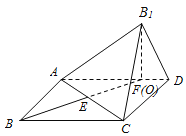
当点O恰好落在![]() 的内部
的内部![]() 不包括边界
不包括边界![]() ,点O恰好在线段EF上,
,点O恰好在线段EF上,
又![]() ,
,![]() ,
,
![]() 为二面角
为二面角![]() 的平面角,
的平面角,
当![]() 时,由
时,由![]() ,可得
,可得![]() ,且
,且![]() ,
,
![]() ,
,
故二面角![]() 的余弦值的取值范围为
的余弦值的取值范围为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目