题目内容
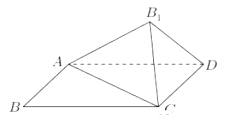
【题目】如图,四棱锥![]() 中,底面ABCD是正方形,平面
中,底面ABCD是正方形,平面![]() 平面ABCD,平面
平面ABCD,平面![]() 平面ABCD.
平面ABCD.
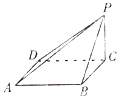
![]() Ⅰ
Ⅰ![]() 证明:
证明:![]() 平面ABCD;
平面ABCD;
![]() Ⅱ
Ⅱ![]() 若二面角
若二面角![]() 的大小为
的大小为![]() ,求PB与平面PAD所成角的大小.
,求PB与平面PAD所成角的大小.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 推导出
推导出![]() 平面PBC,从而
平面PBC,从而![]() ,同理可证
,同理可证![]() ,由此能证明
,由此能证明![]() 平面ABCD.
平面ABCD.![]() Ⅱ
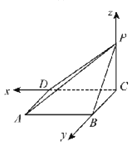
Ⅱ![]() 以C为原点,CD为x轴,CB为y轴,CP为z轴,建立空间直角坐标系,利用向量法能求出PB与平面PAD所成角的大小.
以C为原点,CD为x轴,CB为y轴,CP为z轴,建立空间直角坐标系,利用向量法能求出PB与平面PAD所成角的大小.
证明:![]() Ⅰ
Ⅰ![]() 平面
平面![]() 平面ABCD,平面
平面ABCD,平面![]() 平面
平面![]() ,
,
且![]() ,
,![]() 平面PBC,
平面PBC,![]() ,
,
同理可证![]() ,
,
![]() ,
,![]() 平面ABCD.
平面ABCD.
![]() Ⅱ
Ⅱ![]() 如图,以C为原点,CD为x轴,CB为y轴,CP为z轴,建立空间直角坐标系,
如图,以C为原点,CD为x轴,CB为y轴,CP为z轴,建立空间直角坐标系,
设![]() ,
,![]() ,则
,则![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,
![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
设平面PAB的法向量![]() y,
y,![]() ,
,
则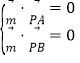 ,即
,即![]() ,取
,取![]() ,得
,得![]() a,
a,![]() ,
,
同理求出平面PAD的法向量![]() 0,
0,![]() ,
,
由![]() ,得
,得![]() ,
,
![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
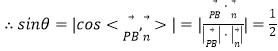 ,
,
![]() 与平面PAD所成角的大小为
与平面PAD所成角的大小为![]() .
.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程![]() (
(![]() 精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
(Ⅱ)从表中的5天中任取一天,若已知所选取该天的热奶茶销售杯数大于120,求所选取该天热奶茶销售杯数大于130的概率.
参考数据:![]() ,
,![]() .参考公式:
.参考公式: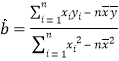 ,
,![]()
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第
人参加“学雷锋”志愿活动,按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有
人参加社区宣传交流活动,求至少有![]() 人年龄在第
人年龄在第![]() 组的概率.
组的概率.