Question

【题目】已知函数。

（1）讨论的单调性；

（2）若的最大值，存在最小值，且，求证：。

Answer 1

【答案】（1）当时，在上单调递减，当时，在单调递增，在单调递减；（2）证明见解析。

【解析】

试题分析：（1）先求，讨论和两种情况，分别令得减区间，得增区间；（2）由（1）可知，且，（为的极值点），由题设，即，将代入上式，得，则。

试题解析：（1）由题设有，当时，在上单调递减；

当时，列表如下：

		0
	递增	最大值	递减

可知，在单调递增，在单调递减；

（2）由题设有，

若，在其定义域上单调递增，无最小值，由（1）可知此时无最大值，故而令，又，

故唯一存在，使得，即，

列表如下

		0
		0
	递减	最小值	递增

由（1）可知，且，由题设，即，将代入上式有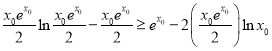，化简得。构造函数，

，易知为单调递增函数，又，而当，则唯一存在，使得，则当递减，当，，递增。又，故只会在有解，而，故（*）的解为，则。