题目内容
【题目】已知![]() .
.
(1)判断函数![]() 的奇偶性并证明;
的奇偶性并证明;
(2)证明![]() 是定义域内的增函数;
是定义域内的增函数;
(3)解不等式![]() .
.
【答案】(1)奇函数,证明详见解析;(2)增函数,证明详见解析;(3)![]() 。
。
【解析】
试题分析:(1)函数![]() 的定义域为R,关于原点对称,
的定义域为R,关于原点对称,![]() ,验证
,验证![]() 的值,
的值,![]() ,所以即
,所以即![]() ,因此函数
,因此函数![]() 为奇函数;
为奇函数;
(2)首先可以将函数化简,即![]() ,根据定义证明函数
,根据定义证明函数![]() 在定义域内为增函数,设
在定义域内为增函数,设![]() 是R上任意两个不等的实数,且
是R上任意两个不等的实数,且![]() ,则
,则![]() ,
,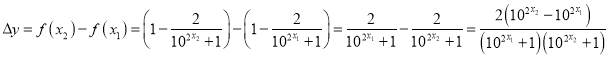 ,由于函数
,由于函数![]() 在R上为增函数,所以当
在R上为增函数,所以当![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,则函数
,则函数![]() 在R上为增函数;(3)由第(1)、(2)问可知函数
在R上为增函数;(3)由第(1)、(2)问可知函数![]() 为奇函数且为增函数,所以
为奇函数且为增函数,所以![]() 转化为
转化为![]() ,即
,即![]() ,所以转化为
,所以转化为![]() ,所以
,所以![]() ,
,![]() ,则
,则![]() 。
。
试题解析:(1)∵![]() 的定义域为R,且
的定义域为R,且![]() ,
,
∴![]() 是奇函数.
是奇函数.
(2)![]()
![]()
![]()
设![]() 且
且![]() ,则
,则
![]()
![]()
![]()
∵![]() 为增函数,∴当
为增函数,∴当![]() 时,
时,![]() ,
,
又∵![]() , ∴
, ∴![]() ,即
,即![]()
∴![]() 在定义域上为增函数.
在定义域上为增函数.
(3) 不等式可化为![]()
由(1)知![]() 是奇函数 ∴
是奇函数 ∴![]()
由(2)知![]() 在定义域上为增函数 ∴
在定义域上为增函数 ∴![]()
解得![]()

练习册系列答案
相关题目