题目内容
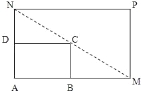
【题目】如下图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米。

(1)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积。
【答案】(1)![]() (2)AN的长为4米,矩形AMPN的面积最小,最小为24米。
(2)AN的长为4米,矩形AMPN的面积最小,最小为24米。
【解析】
试题分析:(1)设AN的长为x,利用![]() ,用x表示AM,然后求面积,
,用x表示AM,然后求面积,![]() ,再解不等式
,再解不等式![]() 求x得范围。(2)解法一:把
求x得范围。(2)解法一:把![]() 中的x-2看成整体变形成
中的x-2看成整体变形成![]() ,用基本不等式求解。解法二:对
,用基本不等式求解。解法二:对![]() 求导,利用导数求极小值即为最小值。
求导,利用导数求极小值即为最小值。
试题解析:解:(1)解:设AN的长为x米(x>2)由题意可知:∵![]() ∴
∴![]() ∴
∴![]() ∴
∴![]() 由SAMPN>32得
由SAMPN>32得![]() ,
,
∵x>2∴3x2﹣32(x﹣2)>0,即(3x﹣8)(x﹣8)>0(x>2)解得:![]() 即AN长的取值范围是
即AN长的取值范围是![]()
(2)
解法一:∵x>2,∴![]()
![]()
当且仅当![]() ,即x=4时,取“=”号即AN的长为4米,矩形AMPN的面积最小,最小为24米。
,即x=4时,取“=”号即AN的长为4米,矩形AMPN的面积最小,最小为24米。
解法二:
∵![]() ∴
∴![]()
令S'=0得x=4当2<x<4时,S'<0当x>4时S'>0
当x=4时,S取极小值,且为最小值。
即AN长为4米时,矩形AMPN的面积最小,最小为24平方米。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目

