题目内容
5.定义域为R的函数f(x)={−2x(x≤0)f(x−1)(0<x≤3)−3(x−4)2+3(x>3),若函数g(x)=f(x)-2x-a有且只有两个零点,则实数a的取值范围为( )| A. | {a|-6≤a<2} | B. | {a|-4≤a<2}∪{-5}∪{-6} | C. | {a|-5≤a<2}∪{-6} | D. | {a|-4≤a<2}∪{-143}∪{-6} |
分析 由题意可知函数f(x)与函数y=2x+a有且只有两个不同的交点,作函数图象,数形结合求解.
解答 解:∵函数g(x)=f(x)-2x-a有且只有两个零点,
∴函数f(x)与函数y=2x+a有且只有两个不同的交点,
作函数f(x)与函数y=2x+a的图象如下,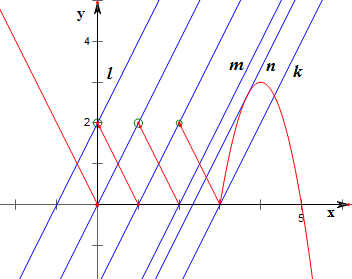
其中红色为线条为函数f(x)的图象,蓝色线条为当a取不同的值时y=2x+a的图象;
直线l时a取2,直线m时a取-4;直线k时a取-6;
直线n是y=-3(x-4)2+3的切线,
故-6(x-4)=2;
故x=4-13,y=3-13;
故a=3-13-2(4-13)=13-5=-143;
综上所述,实数a的取值范围为{a|-4≤a<2}∪{-143}∪{-6};
故选:D.
点评 本题考查了函数的零点与函数图象的交点的应用及数形结合的思想应用,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.由某个2×2列联表数据计算得随机变量K2的观测值k=6.879,则下列说法正确的是( )
| P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 两个分类变量之间有很强的相关关系 | |
| B. | 有99%的把握认为两个分类变量没有关系 | |
| C. | 在犯错误的概率不超过1.0%的前提下认为这两个变量间有关系 | |
| D. | 在犯错误的概率不超过0.5%的前提下认为这两个变量间有关系 |