函数y=0.2-x的反函数是$y=lo{g} {5}^{x}$．题目和参考答案——青夏教育精英家教网——

题目内容

17．函数y=0.2^-x的反函数是$y=lo{g}_{5}^{x}$．

分析先化简函数解析式，再由底数相同的指数函数、对数函数互为反函数，求出原函数的反函数．

解答解：由题意得，y=0.2^-x=5^x，
∴原函数的反函数是：$y=lo{g}_{5}^{x}$，
故答案为：$y=lo{g}_{5}^{x}$．

点评本题考查指数函数的反函数，即底数相同的指数函数、对数函数互为反函数，属于基础题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

7．已知二次函数y=x²-2ax+1在区间（2，3）上是单调函数，则实数a的取值范围是（　　）

a≤-3或a≥-2

8．已知圆C的方程为（x-2）²+（y+1）²=9，若直线l：y=kx+2与圆C相交，求k的取值范围．

5．定义域为R的函数f（x）=$\left\{\begin{array}{l}{-2x（x≤0）}\\{f（x-1）（0＜x≤3）}\\{-3（x-4）^{2}+3（x＞3）}\end{array}\right.$，若函数g（x）=f（x）-2x-a有且只有两个零点，则实数a的取值范围为（　　）

{a|-4≤a＜2}∪{-5}∪{-6}

{a|-5≤a＜2}∪{-6}

{a|-4≤a＜2}∪{-$\frac{14}{3}$}∪{-6}

12．函数y=x³-2x+2过点P（2，6）的切线的斜率为1或10．

2．设α是锐角，sinα=$\frac{4}{5}$．求：
（1）cosα的值；
（2）sin（α+$\frac{π}{3}$）的值．

9．已知函数f（x）=|x+1|，g（x）=m-2|x-4|，若2f（x）≥g（x）恒成立，实数m的最大值为a．
（Ⅰ）求实数a的值；
（Ⅱ）已知实数x，y，z满足x+y+z=a，求2x²+3y²+6z²的最小值．

6．在正四面体ABCD中，点E，F分别是AB，BC的中点，则下列结论错误的是（　　）

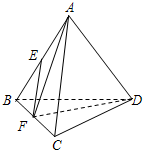
	A．	异面直线AB与CD所成的角为90°		B．	直线AB与平面BCD成的角为60°
	C．	直线EF∥平面ACD		D．	平面AFD垂直平面BCD

7．已知$tan（α+\frac{π}{5}）=2$，$tan（β-\frac{4π}{5}）=-3$，则tan（α-β）=（　　）