题目内容
20.关于△ABC有如下命题:在正三角形ABC内部(不包括边界)任取一点P,P点到三边的距离分别为h1,h2,h3,则h1+h2+h3为定值,证明如下:连接PB、PC、PA,设△PBC、△PCA、△PAB的面积分别为S1,S2,S3,△ABC的面积为S,则有:S=S1+S2+S3⇒h=h1+h2+h3(其中h为△ABC的高),根据上述思维猜想在正四面体(四个面均为正三角形的三棱锥)中的结论,并对猜想进行证明.分析 由平面图形的性质向空间物体的性质进行类比时,常用的思路有:由平面图形中点的性质类比推理出空间里的线的性质,由平面图形中线的性质类比推理出空间中面的性质,由平面图形中面的性质类比推理出空间中体的性质.固我们可以根据已知中平面几何中,关于线的性质“正三角形内任意一点到三边距离之和是一个定值”,推断出一个空间几何中一个关于面的性质
解答 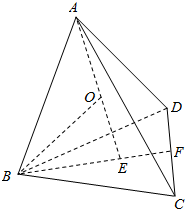 解:类比在正三角形ABC内部(不包括边界)任取一点P,P点到三边的距离分别为h1,h2,h3,则h1+h2+h3为定值,可得:
解:类比在正三角形ABC内部(不包括边界)任取一点P,P点到三边的距离分别为h1,h2,h3,则h1+h2+h3为定值,可得:
P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4为定值,
如图:连接PA,PB,PC,PD,则三棱锥P-ABC,P-ABD,P-ACD,P-BCD的体积分别为:V1,V2,V3,V4,
由棱长为a可以得到BF=$\frac{\sqrt{3}}{2}$a,BE=$\frac{2}{3}$BF=$\frac{\sqrt{3}}{3}$a,
在直角三角形ABE中,根据勾股定理可以得到
AE2=AB2-BE2,即AE=$\frac{\sqrt{6}}{3}$a,即h=$\frac{\sqrt{6}}{3}$a,(其中h为正四面体A-BCD的高),
故正四面体的体积V=$\frac{1}{3}$×$\frac{\sqrt{3}}{4}{a}^{2}$×$\frac{\sqrt{6}}{3}$a=$\frac{\sqrt{2}}{12}{a}^{3}$,
正四面体的四个面△ABC,△ACD,△ABD,△BCD的面积均为$\frac{\sqrt{3}}{4}{a}^{2}$,
则V=V1+V2+V3+V4=$\frac{1}{3}$(h1+h2+h3+h4)$\frac{\sqrt{3}}{4}{a}^{2}$,
解得:h1+h2+h3+h4=$\frac{\sqrt{6}}{3}$a,
∴即P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4为定值$\frac{\sqrt{6}}{3}$a.
点评 本题考查的知识点是类比推理,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
| A. | {0,2} | B. | {(0,2)} | C. | (0,2) | D. | ∅ |
| A. | {a|-6≤a<2} | B. | {a|-4≤a<2}∪{-5}∪{-6} | C. | {a|-5≤a<2}∪{-6} | D. | {a|-4≤a<2}∪{-$\frac{14}{3}$}∪{-6} |
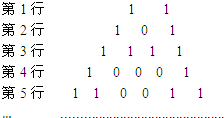 将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.
将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.