题目内容
13.由某个2×2列联表数据计算得随机变量K2的观测值k=6.879,则下列说法正确的是( )| P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 两个分类变量之间有很强的相关关系 | |
| B. | 有99%的把握认为两个分类变量没有关系 | |
| C. | 在犯错误的概率不超过1.0%的前提下认为这两个变量间有关系 | |
| D. | 在犯错误的概率不超过0.5%的前提下认为这两个变量间有关系 |
分析 根据数据计算得随机变量K2的观测值,对照2×2列联表中数据,即可得出统计结论.
解答 解:由2×2列联表数据计算得随机变量K2的观测值是
k=6.879>6.635,
通过对照表中数据得,
在犯错误的概率不超过0.010(即1.0%)的前提下,
认为这两个变量间有关系.
故选:D.
点评 本题考查了应用2×2列联表中的数据,得出统计结论的应用问题,是基础题目.

练习册系列答案
相关题目
1.某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分),其中120分(含120分)以上为优秀,绘制了如下的两个频率分布直方图:
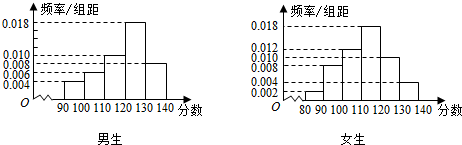
(1)根据如图两个直方图完成2×2列联表:
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?

(1)根据如图两个直方图完成2×2列联表:
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | |||
| 女生 | |||
| 总计 |
| K0 | 2.072 | 2.076 | 3.814 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
5.定义域为R的函数f(x)=$\left\{\begin{array}{l}{-2x(x≤0)}\\{f(x-1)(0<x≤3)}\\{-3(x-4)^{2}+3(x>3)}\end{array}\right.$,若函数g(x)=f(x)-2x-a有且只有两个零点,则实数a的取值范围为( )
| A. | {a|-6≤a<2} | B. | {a|-4≤a<2}∪{-5}∪{-6} | C. | {a|-5≤a<2}∪{-6} | D. | {a|-4≤a<2}∪{-$\frac{14}{3}$}∪{-6} |