题目内容
14.已知函数f(x)=$\frac{1}{2}$x2-$\frac{1}{2}$与函数g(x)=mlnx在点(1,0)处有公共的切线,设h(x)=ax-g(x).(Ⅰ)求m的值;
(Ⅱ)若h(x)在x=2处有极值,求h(x)的单调递减区间;
(Ⅲ)是否存在实数a,使h(x)在区间(0,e]的最小值是3,若存在,求出a的值;若不存在,说明理由.
分析 (Ⅰ)由(1,0)在函数f(x)、g(x)的图象上,得到f′(1)=g′(1),从而求出m的值;
(Ⅱ)先求出函数h(x)的表达式,通过求导得到函数h(x)的单调区间;
(Ⅲ)假设存在实数a,使h(x)=ax-lnx在区间(0,e]上有最小值3,求出h′(x)=a-$\frac{1}{x}$,通过讨论a的范围,结合函数的单调性,从而求出a的值.
解答 解:(Ⅰ)因为f(1)=g(1)=0,
所以(1,0)在函数f(x)、g(x)的图象上,
又f′x)=x,$g'(x)=\frac{m}{x}$
所以f′(1)=1,g′(1)=m,
所以m=1;
(Ⅱ)因为h(x)=ax-g(x)=ax-mlnx,
所以h′(x)=a-$\frac{1}{x}$,
又因为h(x)在x=2处有极值,
所以h′(2)=a-$\frac{1}{2}$=0,
所以$a=\frac{1}{2}$,
经检验,$a=\frac{1}{2}$时,h(x)在x=2处有极值.
所以h(x)=$\frac{1}{2}$x-lnx,
令h′(x)=$\frac{1}{2}$-$\frac{1}{x}$<0,解得:x<2,
因为h(x)的定义域为(0,+∞),
所以0<x<2,
即h(x)的单调递减区间为(0,2).
(Ⅲ)假设存在实数a,使h(x)=ax-lnx在区间(0,e]上有最小值3,
由h′(x)=a-$\frac{1}{x}$,
①当a≤0时,h′(x)<0,h(x)在(0,e]上单调递减,
h(x)min=h(e)=ae-1=3,解得:a=$\frac{4}{e}$,舍去;
②当a>$\frac{1}{e}$即0<$\frac{1}{a}$<e时,h(x)在(0,$\frac{1}{a}$)单调递减,在($\frac{1}{a}$,e]单调递增,
∴h(x)min=h($\frac{1}{a}$)=1+lna=3,解得:a=e2,满足条件,
③当0<a<$\frac{1}{e}$即$\frac{1}{a}$>e时,h′(x)<0,
∴h(x)在(0,e]上单调递减,
h(x)min=h(e)=ae-1=3,解得:a=$\frac{4}{e}$,舍去,
综上,存在实数a=e2,使h(x)在区间(0,e]的最小值是3.
点评 本题考查了函数的单调性,函数的极值问题,考查导数的应用,本题是一道中档题.

 名校课堂系列答案
名校课堂系列答案| A. | {a|-6≤a<2} | B. | {a|-4≤a<2}∪{-5}∪{-6} | C. | {a|-5≤a<2}∪{-6} | D. | {a|-4≤a<2}∪{-$\frac{14}{3}$}∪{-6} |
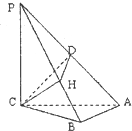 三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )
三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
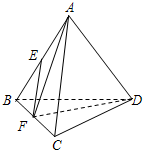
| A. | 异面直线AB与CD所成的角为90° | B. | 直线AB与平面BCD成的角为60° | ||
| C. | 直线EF∥平面ACD | D. | 平面AFD垂直平面BCD |