题目内容
15.若(2x+$\sqrt{3}$)100=a0+a1x+a2x2+…+a100x100,则(a0+a2+a4+…+a100)2-(a1+a3+a5+…+a99)2的值为( )| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
分析 用特殊值,令x=1,得出(2+$\sqrt{3}$)100=a0+a1+a2+…+a100,
x=-1,得出(-2+$\sqrt{3}$)100=a0-a1+a2-…+a100,再因式分解,代入求值即可.
解答 解:∵(2x+$\sqrt{3}$)100=a0+a1x+a2x2+…+a100x100,
∴当x=1时,(2+$\sqrt{3}$)100=a0+a1+a2+…+a100,
当x=-1时,(-2+$\sqrt{3}$)100=a0-a1+a2-…+a100,
∴(a0+a2+a4+…+a100)2-(a1+a3+a5+…+a99)2
=(a0+a1+a2+a3+a4+a5+…+a99+a100)(a0-a1+a2-a3+a4-a5+…-a99+a100)
=(2+$\sqrt{3}$)100×(-2+$\sqrt{3}$)100
=(-4+3)100
=1.
故选:A.
点评 本题考查了二项式定理的应用问题,也考查了因式分解的应用问题,是基础题目.

练习册系列答案
相关题目
5.定义域为R的函数f(x)=$\left\{\begin{array}{l}{-2x(x≤0)}\\{f(x-1)(0<x≤3)}\\{-3(x-4)^{2}+3(x>3)}\end{array}\right.$,若函数g(x)=f(x)-2x-a有且只有两个零点,则实数a的取值范围为( )
| A. | {a|-6≤a<2} | B. | {a|-4≤a<2}∪{-5}∪{-6} | C. | {a|-5≤a<2}∪{-6} | D. | {a|-4≤a<2}∪{-$\frac{14}{3}$}∪{-6} |
6.在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列结论错误的是( )
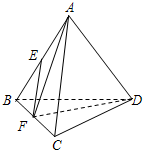

| A. | 异面直线AB与CD所成的角为90° | B. | 直线AB与平面BCD成的角为60° | ||
| C. | 直线EF∥平面ACD | D. | 平面AFD垂直平面BCD |
7.已知$tan(α+\frac{π}{5})=2$,$tan(β-\frac{4π}{5})=-3$,则tan(α-β)=( )
| A. | 1 | B. | -$\frac{5}{7}$ | C. | $\frac{5}{7}$ | D. | -1 |
5.已知定义在实数集R的函数f(x)满足f(1)=4,且f(x)导函数f′(x)<3,则不等式f(lnx)>3lnx+1的解集为( )
| A. | (1,+∞) | B. | (e,+∞) | C. | (0,1) | D. | (0,e) |
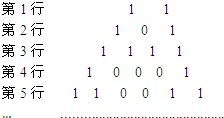 将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.
将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.