题目内容
16.一货船在A处测得灯塔C在北偏东15°且与货船相距20海里,随后货船按北偏西30°方向航行,15分钟后到达B处,此时测得灯塔C在货船的东北方向,若货船的航速为V海里/小时,则V=40($\sqrt{6}$-$\sqrt{2}$).分析 先分别求得∠A和∠B,进而求得∠C,利用正弦定理求得AB,最后除以时间.
解答  解:根据题意知∠BAC=15°+30°=45°,∠CBA=45°+60°=105°,∠C=180°-45°-105°=30°
解:根据题意知∠BAC=15°+30°=45°,∠CBA=45°+60°=105°,∠C=180°-45°-105°=30°
∴sin∠CBA=sin45°cos60°+cos45°sin60°=$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
∴由正弦定理知$\frac{AC}{sinB}$=$\frac{AB}{sinC}$,
∴AB=$\frac{AC}{sinB}$•sinC=$\frac{20}{\frac{\sqrt{2}+\sqrt{6}}{4}}$×$\frac{1}{2}$=10($\sqrt{6}$$-\sqrt{2}$).
V=$\frac{AB}{t}$=$\frac{10(\sqrt{6}-\sqrt{2})}{\frac{1}{4}}$=40($\sqrt{6}$$-\sqrt{2}$)(海里/小时).
即货船的速度为40($\sqrt{6}$$-\sqrt{2}$)海里/小时.
故答案为:$40(\sqrt{6}-\sqrt{2})$.
点评 本题主要考查了正弦定理在解三角形中的应用.考查了学生分析问题和解决实际问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知二次函数y=x2-2ax+1在区间(2,3)上是单调函数,则实数a的取值范围是( )
| A. | a≤-3或a≥-2 | B. | 2≤a≤3 | C. | a≤2或a≥3 | D. | -3≤a≤-2 |
1.某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分),其中120分(含120分)以上为优秀,绘制了如下的两个频率分布直方图:
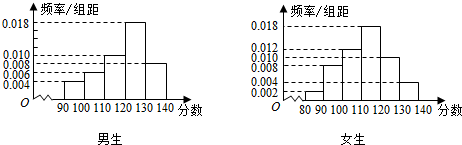
(1)根据如图两个直方图完成2×2列联表:
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?

(1)根据如图两个直方图完成2×2列联表:
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | |||
| 女生 | |||
| 总计 |
| K0 | 2.072 | 2.076 | 3.814 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
5.定义域为R的函数f(x)=$\left\{\begin{array}{l}{-2x(x≤0)}\\{f(x-1)(0<x≤3)}\\{-3(x-4)^{2}+3(x>3)}\end{array}\right.$,若函数g(x)=f(x)-2x-a有且只有两个零点,则实数a的取值范围为( )
| A. | {a|-6≤a<2} | B. | {a|-4≤a<2}∪{-5}∪{-6} | C. | {a|-5≤a<2}∪{-6} | D. | {a|-4≤a<2}∪{-$\frac{14}{3}$}∪{-6} |
6.在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列结论错误的是( )
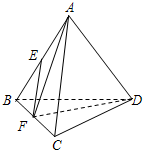

| A. | 异面直线AB与CD所成的角为90° | B. | 直线AB与平面BCD成的角为60° | ||
| C. | 直线EF∥平面ACD | D. | 平面AFD垂直平面BCD |