题目内容
4.已知函数f(x)=$\frac{1}{2}$x2-ax+(a-1)lnx(a>1).(Ⅰ) 讨论函数f(x)的单调性;
(Ⅱ) 若a=2,数列{an}满足an+1=f(an).
(1)若首项a1=10,证明数列{an}为递增数列;
(2)若首项为正整数,且数列{an}为递增数列,求首项a1的最小值.
分析 (Ⅰ)求出函数的导数,并分解因式,对a讨论,当a=2,当1<a<2时,当a>2时,解不等式即可得到单调区间;
(Ⅱ)若a=2,则$f(x)=\frac{1}{2}{x^2}-2x+lnx$,由(Ⅰ)知函数f(x)在区间(0,+∞)上单调递增,
(1)运用数学归纳法即可证得;
(2)由(1)知:当且仅当0<a1<a2,数列{an}为递增数列,f(a1)>a1,即$\frac{1}{2}{a_1}^2-3{a_1}+ln{a_1}>0$(a1为正整数),设$g(x)=\frac{1}{2}{x^2}-3x+lnx$(x≥1),求出导数,运用函数的零点存在定理,即可得到首项的最小值.
解答 解:(Ⅰ)∵$f(x)=\frac{1}{2}{x^2}-ax+({a-1})lnx$,
∴$f'(x)=\frac{{{x^2}-ax+a-1}}{x}=\frac{{({x-1})({x+1-a})}}{x}$(x>0),
当a=2时,则$f'(x)=\frac{{{{({x-1})}^2}}}{x}≥0$在(0,+∞)上恒成立,
当1<a<2时,若x∈(a-1,1),则f′(x)<0,若x∈(0,a-1)或x∈(1,+∞),则f′(x)>0,
当a>2时,若x∈(1,a-1),则f′(x)<0,若x∈(0,1)或x∈(a-1,+∞),则f′(x)>0,
综上所述:当1<a<2时,函数f(x)在区间(a-1,1)上单调递减,
在区间(0,a-1)和(1,+∞)上单调递增;
当a=2时,函数在(0,+∞)上单调递增;
当a>2时,函数f(x)在区间(0,1)上单调递减,在区间(0,1)和(a-1,+∞)上单调递增.
(Ⅱ)若a=2,则$f(x)=\frac{1}{2}{x^2}-2x+lnx$,由(Ⅰ)知函数f(x)在区间(0,+∞)上单调递增,
(1)因为a1=10,所以a2=f(a1)=f(10)=30+ln10,可知a2>a1>0,
假设0<ak<ak+1(k≥1),因为函数f(x)在区间(0,+∞)上单调递增,
∴f(ak+1)>f(ak),即得ak+2>ak+1>0,
由数学归纳法原理知,an+1>an对于一切正整数n都成立,
∴数列{an}为递增数列.
(2)由(1)知:当且仅当0<a1<a2,数列{an}为递增数列,
∴f(a1)>a1,即$\frac{1}{2}{a_1}^2-3{a_1}+ln{a_1}>0$(a1为正整数),
设$g(x)=\frac{1}{2}{x^2}-3x+lnx$(x≥1),则$g'(x)=\frac{{{x^2}-3x+1}}{x}$,
∴函数g(x)在区间$(\frac{{3+\sqrt{5}}}{2},+∞)$上递增,
由于$g(5)=ln5-\frac{5}{2}<0$,g(6)=ln6>0,又a1为正整数,
∴首项a1的最小值为6.
点评 本题考查导数的运用:求单调区间,同时考查函数的零点存在定理和数学归纳法的运用,考查运算能力,属于中档题.

| A. | $\frac{31}{16}$ | B. | $\frac{31}{32}$ | C. | 31 | D. | 15 |
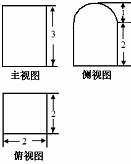
| A. | 20+2π | B. | 20+3π | C. | 24+3π | D. | 24+3π |
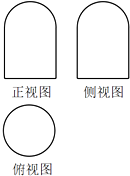 一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为7π.
一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为7π.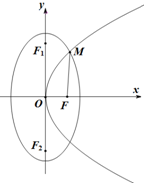 如图,抛物线C1:y2=2px(p>0)与椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{4}$=1(a>2)交于第一象限内一点M,F为抛物线C1的焦点,F1,F2分别为椭圆C2的上下焦点,已知|$\overrightarrow{MF}$-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$.
如图,抛物线C1:y2=2px(p>0)与椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{4}$=1(a>2)交于第一象限内一点M,F为抛物线C1的焦点,F1,F2分别为椭圆C2的上下焦点,已知|$\overrightarrow{MF}$-|$\overrightarrow{OF}$|=1,|$\overrightarrow{MF}$-$\overrightarrow{OF}$|=$\sqrt{10}$.