题目内容
12．已知数列{an}为递增等比数列，其前n项和为Sn．若a1=1，2an+1+2an-1=5an（n≥2），则S5=（ ）| A． | $\frac{31}{16}$ | B． | $\frac{31}{32}$ | C． | 31 | D． | 15 |
分析 通过设an=qn-1（q＞1），利用2an+2+2an=5an+1，计算可得q=2，进而可得结论．
解答 解：设数列{an}的公比为q（q＞1），则an=1×qn-1=qn-1，
∵2an+1+2an-1=5an（n≥2），
∴2an+2+2an=5an+1，
∴2qn+1+2qn-1=5qn，
即：2q2+2=5q，解得q=2或$\frac{1}{2}$（舍），
∴数列{an}是以1为首项，2为公比的等比数列，
∴S5=$\frac{1-{2}^{5}}{1-2}$=31，
故选：C．
点评 本题考查求数列的通项，注意解题方法的积累，属于中档题．
练习册系列答案
特高级教师点拨系列答案
相关题目
3．如图所示，在正方形OABC中任取一点，则该点落在阴影部分的概率为（ ）
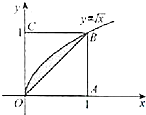
| A． | $\frac{1}{7}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{4}$ |
20．在△ABC中，E、F分别为AB、AC上的点，且AE：EB=AF：FC=1：2，P为EF上任一点，实数x、y满足$\overrightarrow{PA}$+x$\overrightarrow{PB}$+y$\overrightarrow{PC}$=$\overrightarrow{0}$，设△ABC、△PBC、△PCA、△PAB的面积分别为S、S1、S2、S3，记$\frac{{S}_{1}}{S}$=λ1，$\frac{{S}_{2}}{S}$=λ2，$\frac{{S}_{3}}{S}$=λ3，则当λ2•λ3取最大值时，2x+y的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | 1 | D． | $\frac{3}{2}$ |
17．对于定义在R上的函数f（x），若存在x0使得$\underset{\underbrace{f（f…（f（{x}_{0}）））}}{k}$=x0（*），其中k为某个正整数，则称x0为函数f（x）的一个周期点，使得（*）式成立的正整数k称为x0的周期，使得（*）式成立的最小正整数k称为x0的最小周期，若函数f（x）=1-|2x-1|，则函数f（x）（ ）
| A． | 恰有一个最小周期为1的周期点，恰有一个最小周期为2的周期点 | |
| B． | 恰有一个最小周期为1的周期点，恰有两个最小周期为2的周期点 | |
| C． | 恰有两个最小周期为1的周期点，恰有两个最小周期为2的周期点 | |
| D． | 恰有两个最小周期为1的周期点，恰有四个最小周期为2的周期点 |
1．
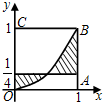如图，正方形OABC的边长为1，记曲线y=x2和直线$y=\frac{1}{4}$，x=1，x=0所围成的图形（阴影部分）为Ω，若向正方形OABC内任意投一点M，则点M落在区域Ω内的概率为（ ）
如图，正方形OABC的边长为1，记曲线y=x2和直线$y=\frac{1}{4}$，x=1，x=0所围成的图形（阴影部分）为Ω，若向正方形OABC内任意投一点M，则点M落在区域Ω内的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{5}$ |